Content
Rules of Integration for Indefinite
Integral
Integration by Parts for
Indefinite Integral
Integration by Parts:
Techniques of
Integration by Parts:
Rules of Integration for Indefinite Integral
In order to simplify the task of finding integrals, some integration techniques are developed to help finding integrals by transforming the integral into two parts.
Integration by Parts for Indefinite Integral
Integration by part is method of transforming the original integral of product of two functions into two integrals for taking the advantage of substitution or transformion of the integral to an easier form to continue the integration. The strategy is to simplify the integral by transforming the original integral into two parts which allowing the integration to be continued in other easier way. The technique is making use of the Rule of Product of Functions in differentiation. i.e.
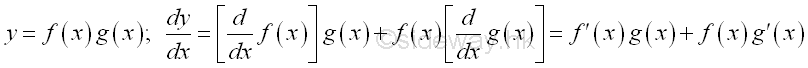
Imply
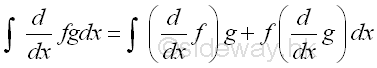
Integration by Parts:
The strategy of the method is making use of Rule of Product of Functions in differentiation for transforming the integral to two suitable formats to continue the integration.
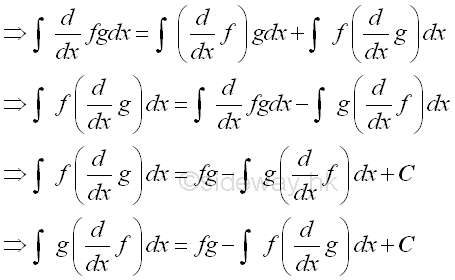
As in reverse substitution, the formula is assumed the substitution is already there, but through the formula of transformation, the assumed substitued function is changed from the first function to the second or vice versa. In other words, the assumed substitued function becomes selectable after the transformation processes. The two processes of transformation are:
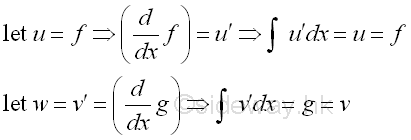
Substitute back. Imply:
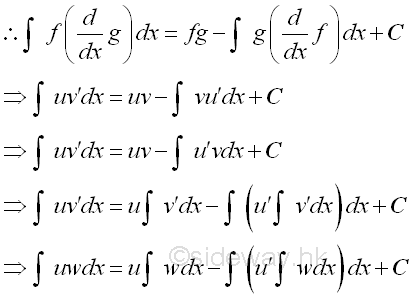
The two functions of the original integrand are interchangable because of the cummutative property of function multiplications. The strategy of the method is making use of the applying of the differentiation operation to one function and the integration operation to the other function in the original integrand so that the integration of the transformed integrand can be continued.
Besides through variable of integration transformation, the formula can be applied for single function also and therefore the integration by parts can be used as formula for the interchanging of variable of integration, imply
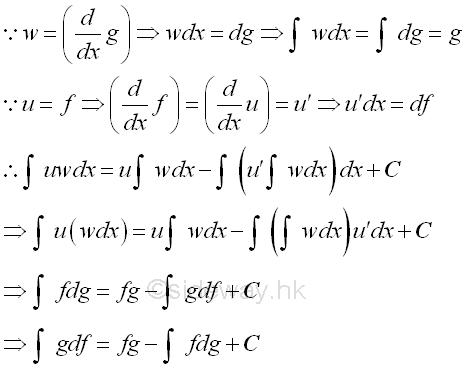
Techniques of Integration by Parts:
-
Single Function.
Method of integration by parts can also be applied for single function by assuming unity as the second function. Imply
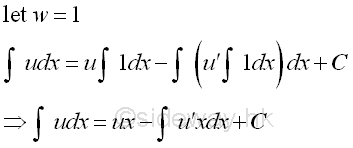
Sometimes the creation of x may help to continue the integration process.
-
Integrand with one function can not be integrated by ordinary means and one function can be integrated by normal means.
Let u be the function which cannot be integrated by ordinary means. And let w be the function that can be integrated by nomral means. Imply
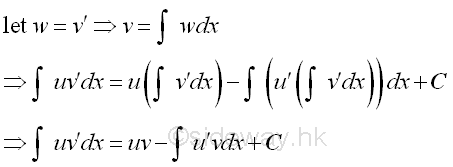
This is the basic idea of integration by parts of making the integration can be continued.
-
If both functions of Integrand are integratable, and one of the function is a function of powers of x, in which the power is positive integer.
Let u be the function of power of x. And let w be the other function. Imply

The function of power of x with positive integer can be eliminated by repeating the application of integration by parts process.
-
If both functions of Integrand are integratable, and one of the function is a function of powers of sin x or cos x.
The power of sin x or cos x can be converted using basic trigonometric identities into linear algebraic expression in terms of sin and cos that the integration by parts can be applied. The basic trigonometric identities are
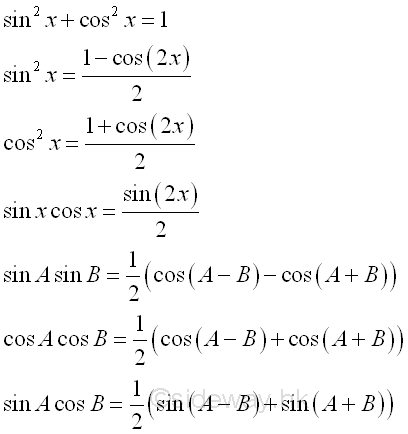
After thAfter the convertion, the function with powers of sin x or cos x become integratable.
-
If the original integral occurs in the result of integration by parts, then the integral can be obtained by algebraic methed indirectly.
Sometimes the original integral occurs in the result of integration by parts after repeatedly using integration by parts, imply
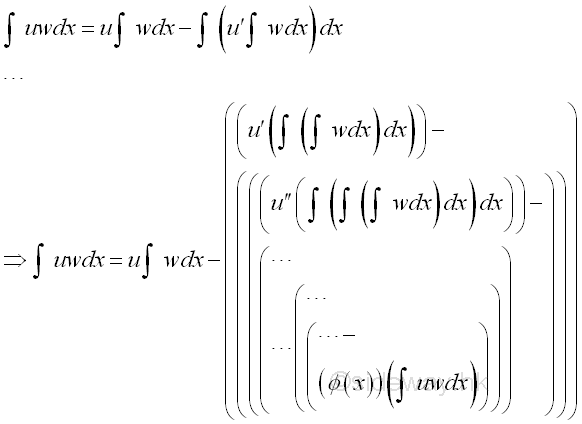
Therefore the integral can be obtained by algebraic method, imply
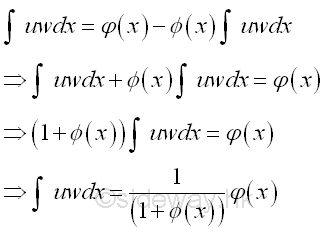
-
If the integral is a power of sin or cos function in which the power is positive integer.
The techniques 4 and 5 of integration by parts can be applied.
-
power of sin function in which the power is positive integer, imply
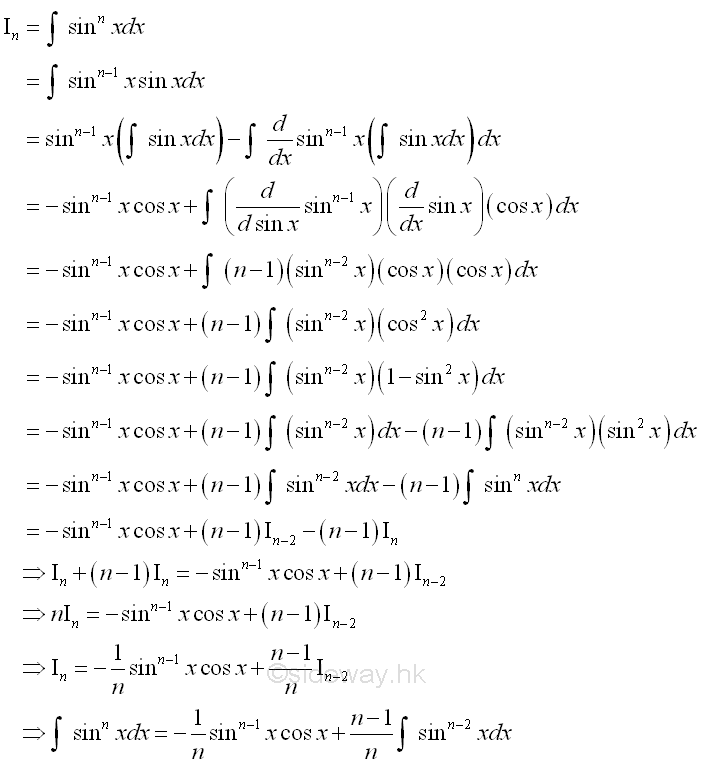
-
power of cos function in which the power is positive integer, imply
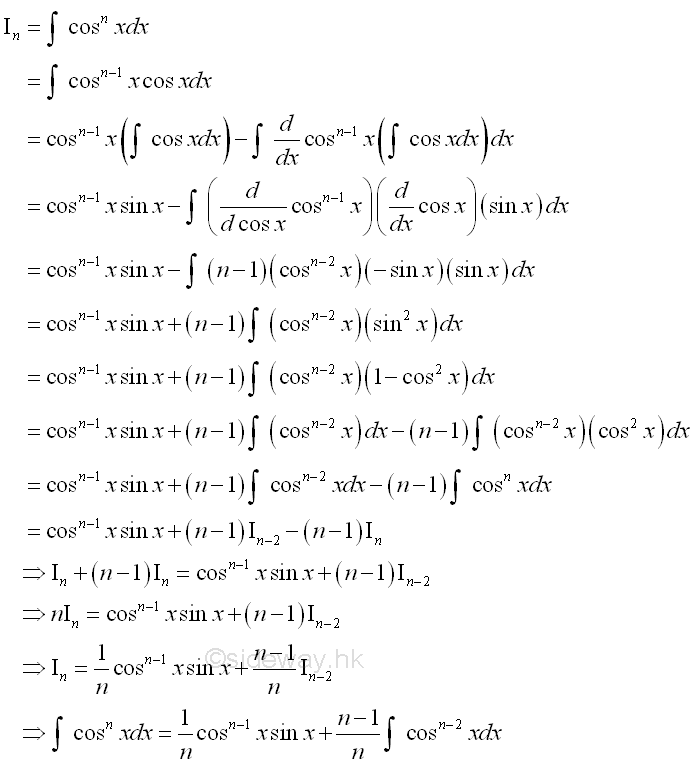
-
©sideway
ID: 111000034 Last Updated: 10/30/2011 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
