Content
Rules of Integration for Improper
Integral
Improper Integral of
Infinite Interval
Improper Integral of Discontinuous Integrand
Convergent & Divergent of Improper Integral
Rules of Integration for Improper Integral
A proper definite integral is the integral of a function f(x) is defined over a finite interval [a,b] and the function f(x) is a bounded continuous function so that the integral of the function always exist. There are also improper definite integrals that the integral of the function f(x) is not defined over a finite interval of the form [a,∞), {-∞,b] or (-∞,∞), or the function f(x) of the integration have infinite discontinuity, e.g. f(a)=,∞,f(b)=,-∞, that the function is not a bounded continuous function on the interval [a,b]. The integral of the first case is named improper integral of type 1. The integral of the second case is named improper integral of type 2.
Improper Integral of Infinite Interval
For an improper integral of a function f(x) with an infinite interval, since the function is continuous and defined for all x in the interval, if the infinity limit of the interval is replaced by a number c which lies between the interval, the integral of the function becomes integrable over the new interval. By the concept of limit, the integral of the function over the finite interval will be equal to the integral of the function over infinite interval when the limit of the integral over the finite interval with the number c exist as the number c approaches infinity. In other words, the improper integal of a function f(x) with an infinite interval is converge and can be converged to a finite number, or the improper integral is convergent. Otherwise, the improper integral is diverge with no limit exist, or the improper integral is divergent. For improper integral with infinity upper limit, imply

For improper integral with infinity lower limit, imply
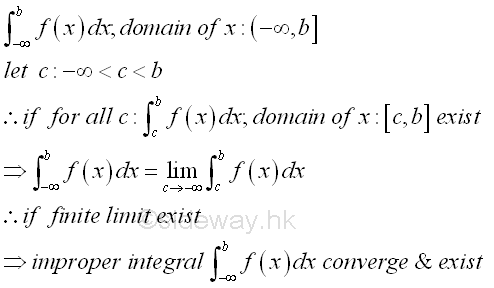
The improper integral with infinity upper and lower limits, the improper integral can be transformed into the former two cases by the definite integral property of additivity of intervals. For the improper integral, in order to be convergent, both transformed proper integrals should be converge and exist. Imply
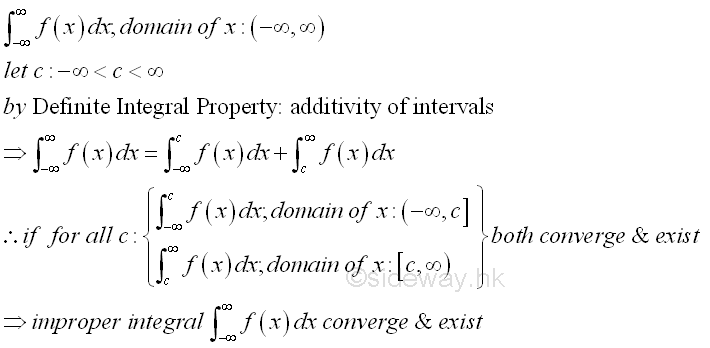
Improper Integral of Discontinuous Integrand
For an improper integral with discontinuous integrand, function f(x) over an finite interval, since the function is continuous and defined for all x in the interval except on the points of discontinuity, similar strategy used in type 1 improper integral can also be applied to the type 2 improper integral of discontinuous integrand by considering the discontinuous point as the infinity point of the interval. If the point of discontinuity of the interval is replaced by a number c which lies between the interval, the integral of the function becomes integrable over the new interval. By the concept of limit, the integral of the continuous function over the finite interval will be equal to the integral of the function over the interval with point of discontinuity when the limit of the integral over the finite interval with the number s exist as the number c approaches the discontinuous point. In other words, the improper integal of a function f(x) with discontinuous point is converge and can be converged to a finite number, or the improper integral is convergent. Otherwise, the improper integral is diverge with no limit exist, or the improper integral is divergent. For improper integral with point of discontinuity at upper limit, imply

For improper integral with point of discontinuity at lower limit imply
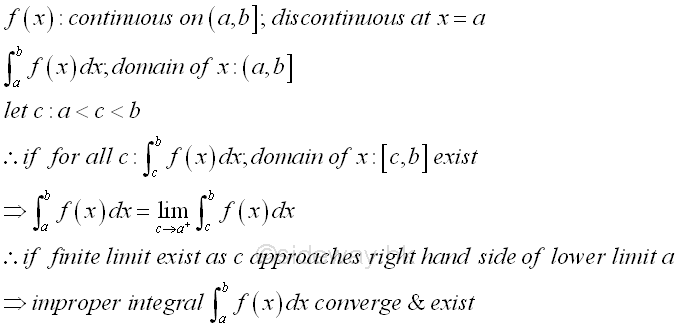
The improper integral with points of discontinuity at upper and lower limits, the improper integral can be transformed into the former two cases by the definite integral property of additivity of intervals. For the improper integral, in order to be convergent, both transformed proper integrals should be converge and exist. Imply

Similarly, if the improper integral with point of discontinuity in between the upper and lower limits, the improper integral can also be transformed into the former two cases by the definite integral property of additivity of intervals. For the improper integral, in order to be convergent, both transformed proper integrals should also be converge and exist. Imply

Convergent & Divergent of Improper Integral
One of the most important concerns of improper integral is the convergence of the improper integral. For the case of type 1 improper integral, when the finite limit L of the improper integral exists, the improper integral is said to be converge to limit L and the improper integral is convergent. However, if the limit of the improper integral is infinity of either positive of negative, the improper integral is said to be diverge to infinity or minus infinity and the improper integral is divergent. One of the effective way to determine the convergency is the comparison test by comparing with an improper integral that is known to be convergent or divergent. When considering an integral as the signed area under the curve of a function, for example, if for all x, the function f(x) is larger than or equal to the function g(x) and functions f(x) and g(x) are greater than or equal to zero, the area of the known improper integral of function f(x) always bound the area of an improper integral of function g(x), therefore if the area of the improper integral of function f(x) is finite or the improper integral of function f(x) is converge, the area of the improper integral of the function g(x) must be finite or the improper integral of function g(x) is converge also. However if the function f(x) is smaller than the function g(x) for all x, the area of the known improper integral of function f(x) is always bounded by the area of an improper integral of function g(x), therefore if the area of the improper integral of function f(x) is infinite or the the improper integral of function f(x) is diverge, the area of the improper integral of the function g(x) must be infinite or the improper integral of the function g(x) is diverge also. Imply
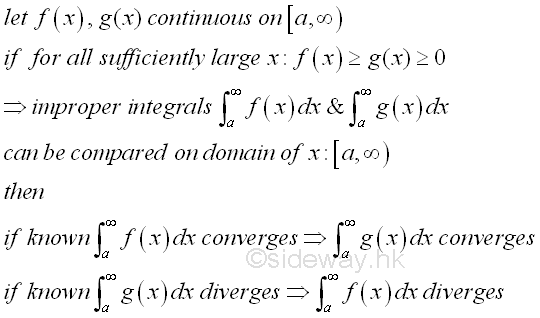
Since signed area is used in the comparison test, the values of both functions f(x) and g(x) should be of the same sign. Similarly, the comparison test can also be applied to other cases of the improper integrals of type 1.
Besides, the comparison test can also be extended to test the convergence of the improper integral of discontinuous integrand by selecting an suitable function to test the convergence of the improper integral near the point of discontinuity. Sometimes, the discontinuous interval can be tested separately using subtraction of intervals. for example, if for all x near the point of distinuity, the function f(x) is larger than or equal to the function g(x) and functions f(x) and g(x) are greater than or equal to zero, the area of the known improper integral of function f(x) always bound the area of an improper integral of function g(x), therefore if the area of the improper integral of function f(x) is finite or the improper integral of function f(x) is converge, the area of the improper integral of the function g(x) must be finite or the improper integral of function g(x) is converge also. However if the function f(x) is smaller than the function g(x) for all x near the point of distinuity, the area of the known improper integral of function f(x) is always bounded by the area of an improper integral of function g(x), therefore if the area of the improper integral of function f(x) is infinite or the the improper integral of function f(x) is diverge, the area of the improper integral of the function g(x) must be infinite or the improper integral of the function g(x) is diverge also. Imply
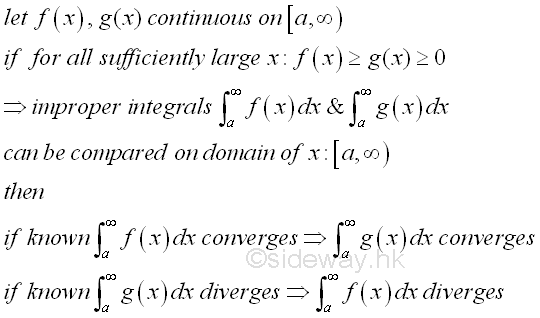
©sideway
ID: 130200001 Last Updated: 2/5/2013 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)
- Tefal BL83SD PerfectMix Cook Blender(last updated On 11/25/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/24/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/23/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/22/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
