Content
Rules of Integration for Indefinite
Integral
Method of Partial Fractions for
Indefinite Integral
Partial Fraction Decomposition:
Denominator Factorization
Method of Factorization
Rules of Integration for Indefinite Integral
In order to simplify the task of finding integrals, some integration techniques are used to help finding integrals by converting the integrand into some simple integrands.
Method of Partial Fractions for Indefinite Integral
The technique of Integration by Partial Fractions is method of decomposing the original integrand of the rational function format into the sum of some simple algebraic fractions with its denominator becomes simple polynomial function. The strategy is to break down the calculation work from determine the integral of a rational function with complex format into the sum of a finite number of integrals of simple algebraic fractions. Therefore the integrand of the integral is expressed in partial fractions before proceeding to determine the value of the integral of the orginal integrand. Imply
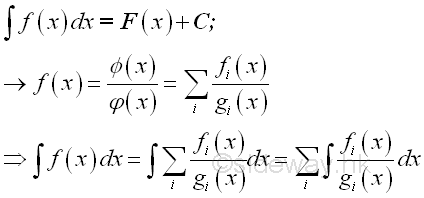
where Φ(x) and φ(x) are rational, integral, algebraical functions of x
Partial Fraction Decomposition:
The method of partial fraction decomposition can be applied to all rational functions with the degree of its numerator is less than the degree of its denominator. Therefore polynomial long division may be used to resolve the problem of improper fractions. imply
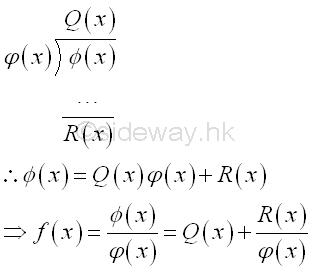
where Q(x) is quotient polynomial, R(x) is remainder polynomial with degree less than the degree of the denominator φ(x). And with the nominator Φ(x) is the dividend and the denominator φ(x) is the divisor, i.e dividend=divisor x quotient + remainder.
Denominator Factorization
After converting the rational function of the integrand to a proper fraction for partial fractions, the polynomial of the denominator can then be factored completely, that is no factoring of the polynomial of the denominator can be carried further. The factorized denominator is a product of either be monomial or binomial of the linear form ax+b or irreducible trinomial of the quadratic form ax2+bx+c. An irreducible trinomial is a prime if and only if the quadratic has no real roots. When the quadratic has a root x1, then x-x1 must be the factor of the quadratic.
An irreducible trinomial can be checked using the quadratic formula:
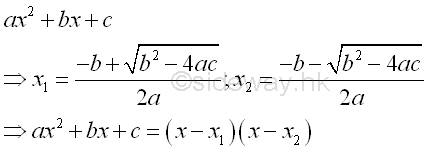
Therefore when b2-4ac>=0, the roots are real numbers and the trinomial can be factored. And thus the trinomial is irreducible if and only if the discriminant b2-4ac<0.
The integrand after denominator factorization is
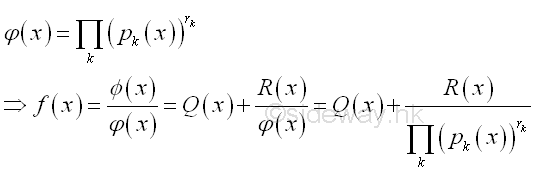
Method of Factorization
Methods to examine and to determine the factors of a polyonomial are:
-
Factor out the greatest common factor of the polyonomial by determining the largest monomial that can divide each term of the polynomial and removing out the common factor from the original polyonomial.
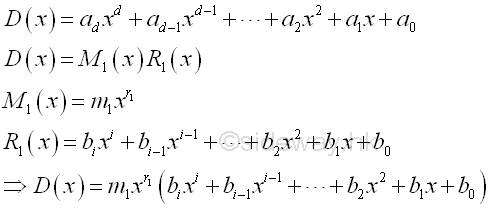
-
Identify common factors of the remaining polynomial by grouping terms together in a regular pattern.
-
scanning for common binomial if the number of terms in the polynomial is even.
-
Group terms in the polynomial into pairs with a common factor that is to group two terms in the polynomial with a regular pattern so that the degree difference of terms in a group is the same for all groups and the difference between paried terms is the monomial factors only.
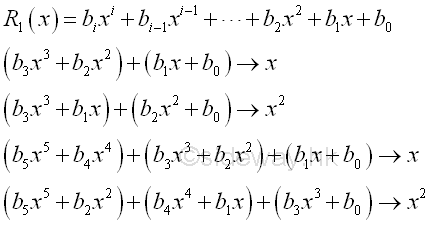
Therefore the polynomial can be expressed as
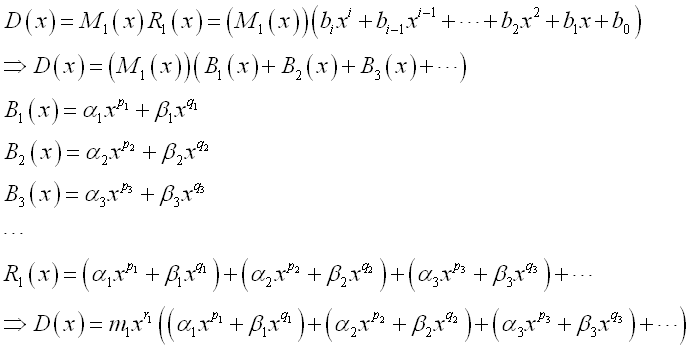
-
Factor out the greatest common factor of each individual grouped binomial by determining the largest monomial that can divide each term of the individual grouped binomial seperately.
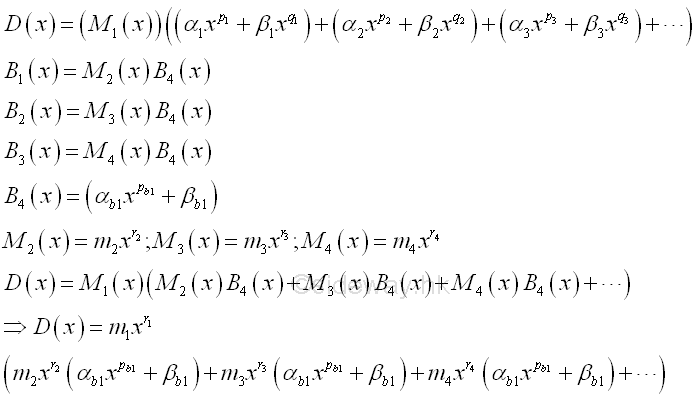
-
Factor out the common binomial
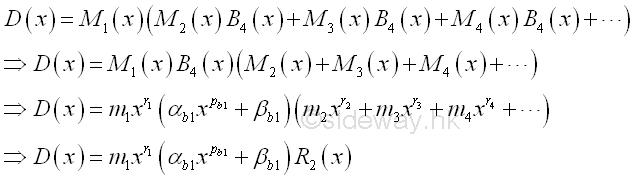
-
Repeat factoring out the common binomial from the remaining polynomial whenever possible.
-
-
scanning for common trinomial if the number of terms in the polynomial is odd and greater or equal to three.
-
If the number of terms in the polynomial is equal to three, try the standard factor trinomial factor into factors first so as to factor as a product of two binomial.
-
Applying the technique of reverse FOIL method, e.g. Last-Inner-Outer-First product, to determine the common trinomial factors, i.e. prime or irreducible quadratic polynomials.
-
-
-
Factor standard binomial factor into factors
-
form a2-b2
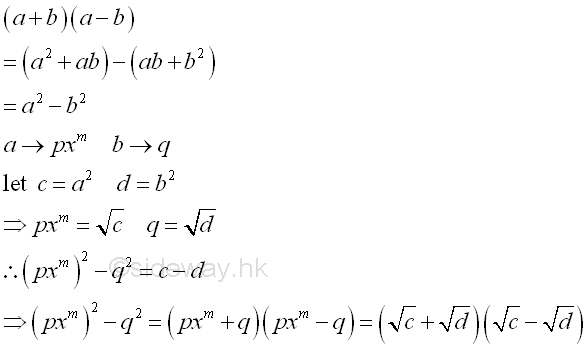
Therefore the degree of binomial is multiple of two with coefficients of opposite sign can be applied. Repeat factoring whenever possible.
-
form a3-b3
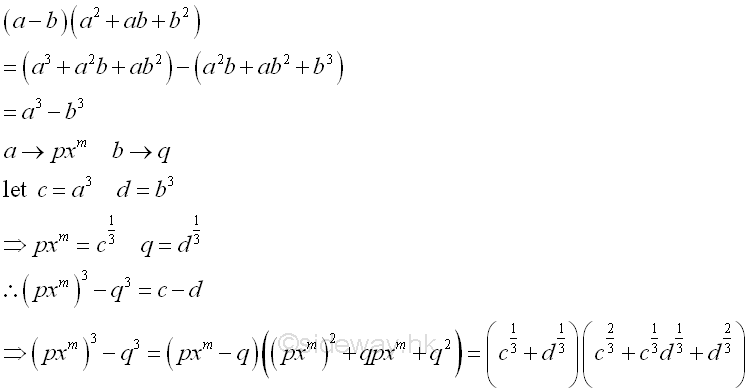
Therefore the degree of binomial is multiple of three with coefficients of opposite sign can be applied. Repeat factoring whenever possible.
-
form a3+b3
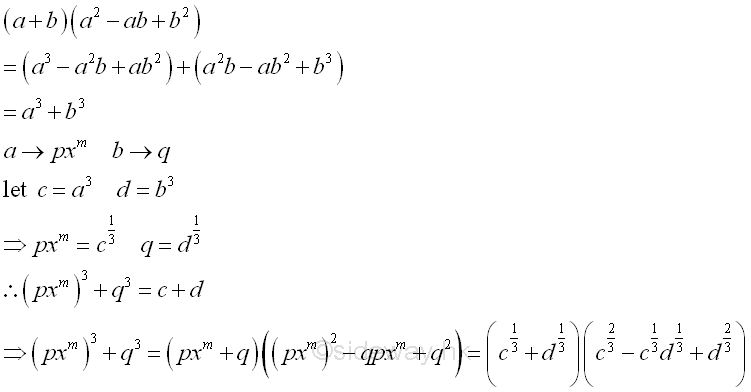
Therefore the degree of binomial is multiple of three with coefficients of equal sign can be applied. Repeat factoring whenever possible.
-
form a4-b4
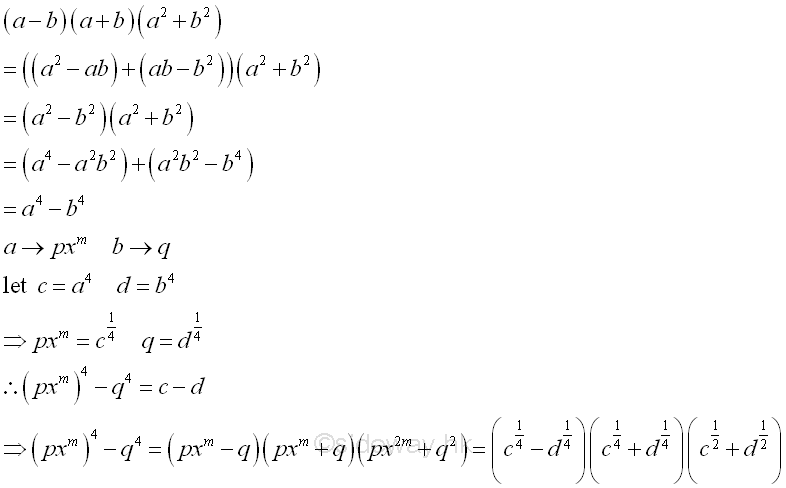
This is the special case of type a. Repeat factoring whenever possible.
-
-
Factor standard polynomial factor into standard binomial factors.
Sometimes the polynomial can be factorized into product of binomial factors. Following are some standard polynomial pa4+qa3+ra2+sa+t for reference.
-
Factor trinomial factor into product of binomial factors
-
standard form a2-2ab+b2 or standard format ra2+sa+t
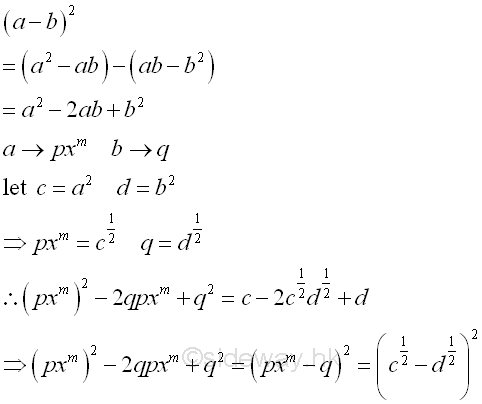
Therefore test for the squares and product of coefficients, the standrad trinomial, a perfect square trinomial, can be factored to the square of a binomial. Repeat factoring whenever possible.
-
standard form a2+ab+b2 or standard format ra2+sa+t
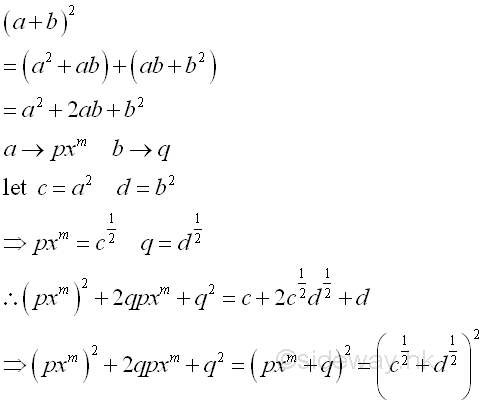
Therefore test for the squares and product of coefficients, the standrad trinomial, a perfect square trinomial, can be factored to the square of a binomial. Repeat factoring whenever possible.
-
form a2+ca+d or standard format ra2+sa+t
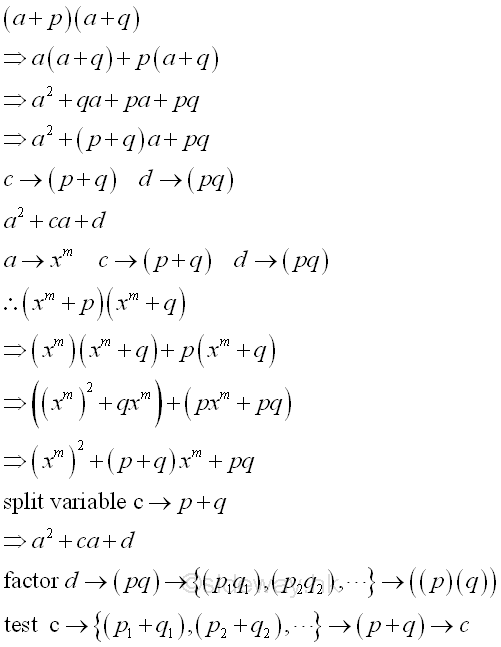
Therefore the coefficient of the highest degree of the tribomial is eqaul to 1. The trinomial can be transformed to a four terms polynomial for grouping factorization by spliting the middle variable c into two terms. Or the trinomial can be factored by trial and error by factoring the constant d to all possible product pair set and testing the sum of each set with the coefficient c. Repeat factoring whenever possible.
-
form ba2+ca+d or standard format ra2+sa+t
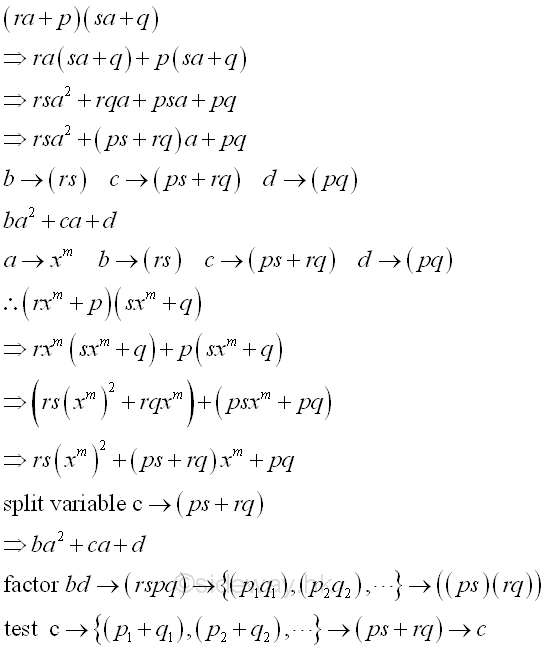
Therefore the coefficient of the highest degree of the tribomial is greater than 1. The trinomial can be transformed to a four terms polynomial for grouping factorization by spliting the middle variable c into two terms. Or the trinomial can be factored by trial and error by factoring the constant d to all possible product pair set and testing the sum of each set with the coefficient c. Repeat factoring whenever possible.
-
-
Factor standard quadrinomial factor into product of binomial factors.
-
form a3-3a2b+3ab2-b3 or standard polynomial qa3+ra2+sa+t
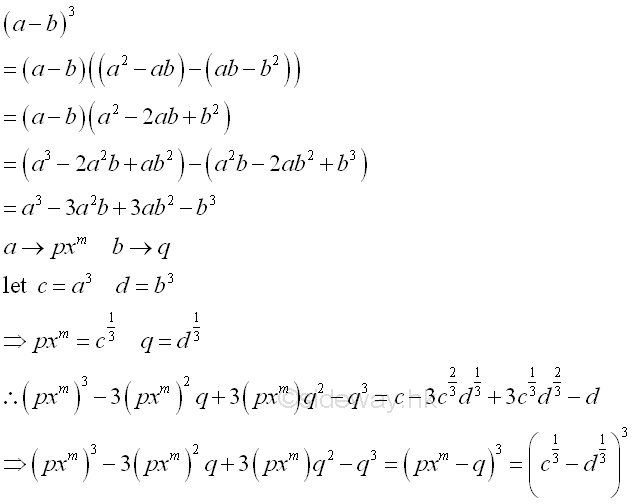
-
form a3+3a2b+3ab2+b3 or standard polynomial qa3+ra2+sa+t
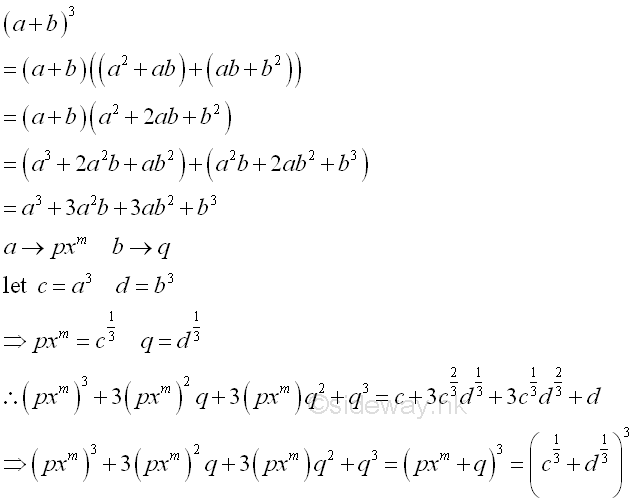
Therefore the coefficient of the highest degree of a standard quadrinomial is 3 with same coefficient format can be applied. Repeat factoring whenever possible.enever possible.
-
-
Factor standard quintinomial factor into product of binomial factors.
-
form a4-3a2b+3ab2+3ab2-b3 or standard polynomial pa4+qa3+ra2+sa+t
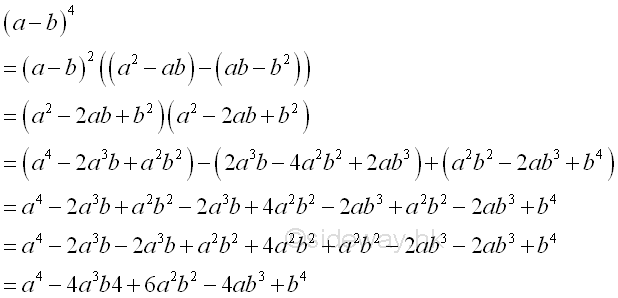
-
form a3+3a2b+3ab2+b3 or standard polynomial pa4+qa3+ra2+sa+t
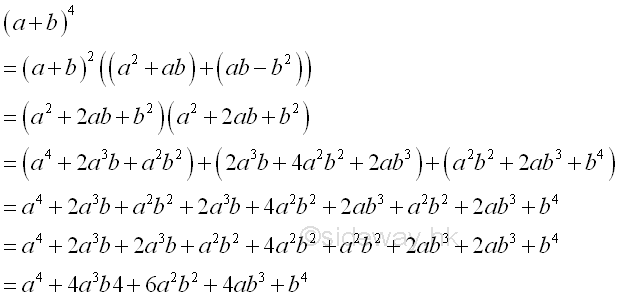
Therefore the coefficient of the highest degree of a standard quadrinomial is 3 with same coefficient format can be applied. Repeat factoring whenever possible.enever possible.
-
-
-
Factor standard polynomial factor into standard trinomial factors.
Sometimes the polynomial can be factorized into product of trinomial factors. Following are some standard polynomial pa4+qa3+ra2+sa+t for reference.
-
Factor trinomial factor into standard trinomial factors.
form pa4-ra2+t ; b2>2c
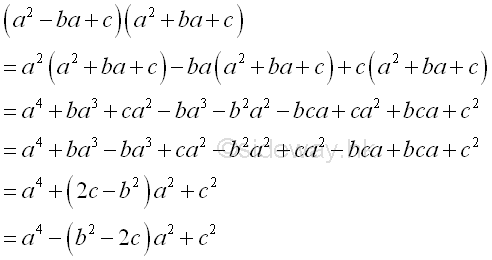
-
Factor quadrinomial factor into standard trinomial factors.
-
form -pa4+ra2+sa+t
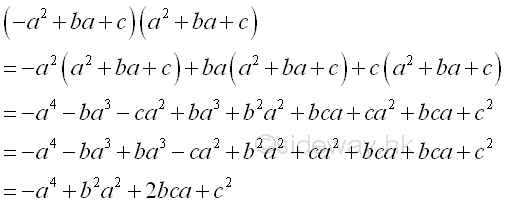
-
form pa4+qa3+ra2-t
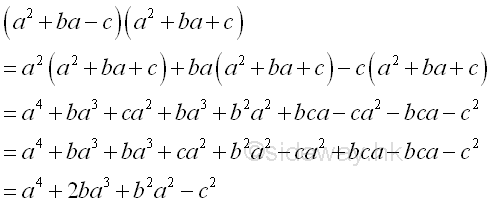
-
-
Factor quintinomial factor into standard trinomial factors.
-
form pa4+qa3+ra2+sa+t
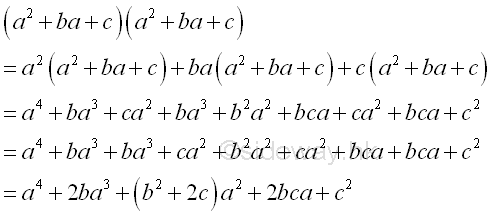
-
form pa4-qa3+ra2+sa+t ; b2>2c
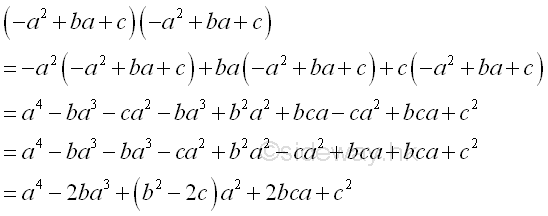
-
form pa4-qa3+ra2-sa+t
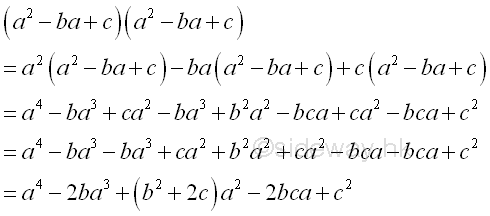
-
form pa4+qa3+ra2-sa+t ; b2>2c
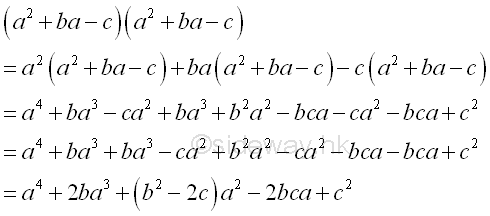
-
-
©sideway
ID: 111000026 Last Updated: 10/26/2011 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Pentium(last updated On 7/3/2025)
- Intel CPU(last updated On 7/2/2025)
- Intel CPU History(last updated On 7/1/2025)
- FreeGLUT Windows Function(last updated On 1/27/2025)
- FreeGLUT Initialization Function(last updated On 1/26/2025)
- FreeGLUT(last updated On 1/25/2025)
- GLUT(last updated On 1/24/2025)
- OpenGL(last updated On 1/23/2025)
- XPower UC140 4-Port 140W PD3.1 GaN Travel Charger(last updated On 1/22/2025)
- XPower DX6 6 In 1 (2x3) 60W PD3.0 Sync & Charge Cable(last updated On 1/21/2025)
- XPower MF240 1.2M Magnetic Absorption 4 in 1 (2x2) Zinc Alloy 240W PD Sync & Charge Cable(last updated On 1/20/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Computer
Hardware 257
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
