Content
Bounded Area of a Function
Bounded Area of a Curve which is entirely above the x-axis
Bounded Area of a Curve which is entirely
below the x-axis
Bounded Area of a Curve which is partly
above and partly below the x-axis
Net Bounded Area of a function:
Total Bounded Area of a function:
Bounded Area of a Curve through transformation
Geometrical Representation of Integration by Parts:
Bounded Area of a Function
Definite integral can be interpreted as the net signed area of the curve bounded by the curve of function f(x) and the x-axis on the closed interval [a,b].
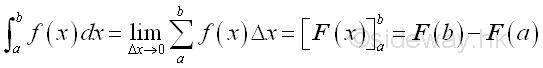
Since Δx is always positive, each infinitesimal element of area will have the same sign as the value of function f(x). The infinitesimal element of area can be positive, negative or zero. The infinitesimal element of area is called the signed area under the curve because the positive area is under the curve and the negative area is above the curve. Therefore the summation of all infinitesimal elements is the net signed bounded area. And for problems of calculating the total bounded area of a function or concerning with the sign of the infinitesimal elements, the shape of the curve should be determined before applying the method of integration.
Bounded Area of a Curve which is entirely above the x-axis
When the curve of a function f(x) is entirely above the x-axis, the area obtained by integration is positive and all infinitesimal elements are under the curve.
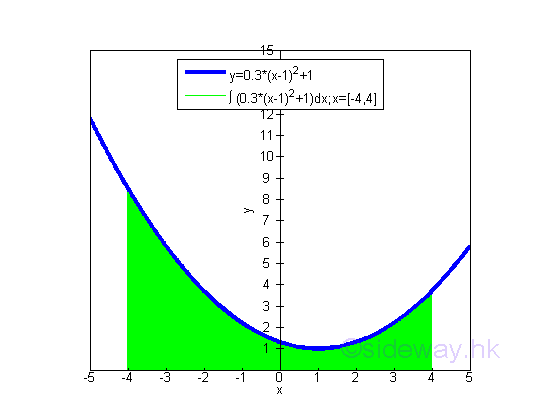
The bounded area underneath the curve of function y=0.3(x-1)2+1 between the closed interval -4 and 4 and above the x-axis is
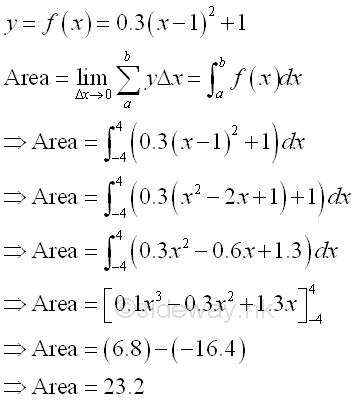
The bounded area under the curve and above the x-axis is positive and is equal to 23.2. But the integral of a function can be positive, negative or zero.
Bounded Area of a Curve which is entirely below the x-axis
When the curve of a function f(x) is entirely below the x-axis, the area obtained by integration is negative and all infinitesimal elements are above the curve.
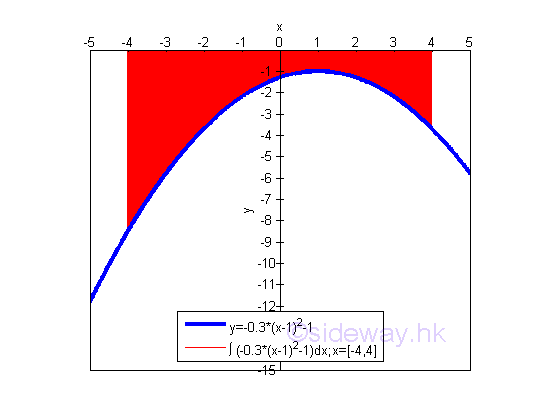
The bounded area above the curve of function y=-0.3(x-1)2-1 between the closed interval -4 and 4 and below x-axis is
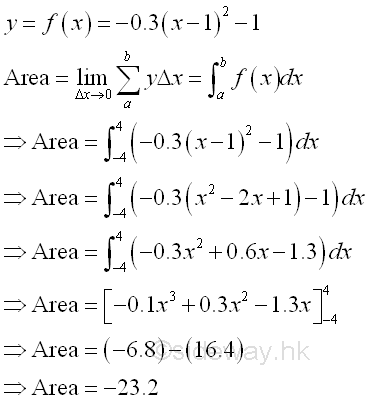
The bounded area above the curve and below the x-axis is negative and is equal to -23.2. The area is the absolute value of the signed area. But the integral of a function can be positive, negative or zero.
Bounded Area of a Curve which is partly above and partly below the x-axis
When the curve of a function f(x) is partly above and partly below the x-axis, the area obtained by integration is the net signed bounded area because the infinitesimal elements can be under or above the curve.
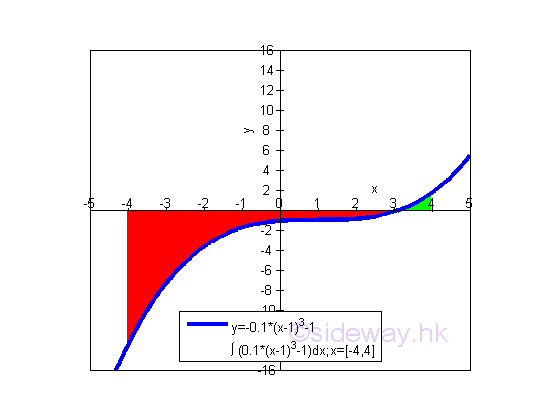
Net Bounded Area of a function:
The net bounded area under the curve of function y=0.1(x-1)3-1 between the closed interval -4 and 4 of x axis is
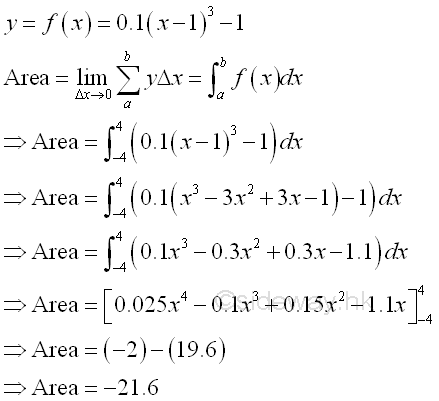
The net bounded area bounded by the curve and the x-axis is negative and is equal to -21.6. The area is the absolute value of the signed area. But the integral of a function can be positive, negative or zero.
Total Bounded Area of a function:
In order to calculate the total bounded area, the shape of the function f(x) should be determined first. The x-intersect of f(x) when y=0 is equal to
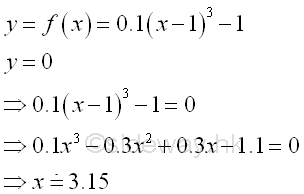
The bounded area bounded by the curve and below the x-axis is
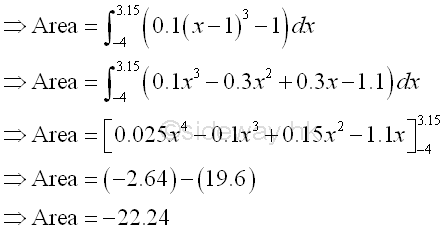
The bounded area bounded by the curve and above the x-axis is
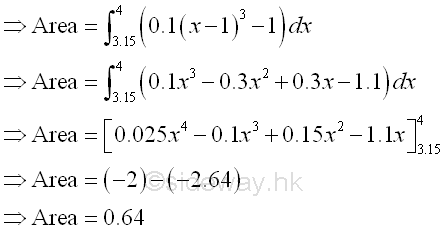
Therefore the net bounded area bounded by the curve is -22.24+0.64=-21.6 as before and the total bounded area bounded by the curve is the sum of absolute area, i.e. 22.24+0.64=22.88
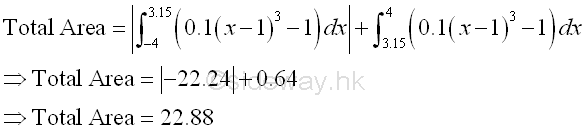
Bounded Area of a Curve through transformation
Since finding the bounded area involving the finding of integral, sometimes finding the bounded area of a curve is much easier to sum vertically than to sum horizontally, that is using an easier way of finding the integral.
And mathematically, the relationship between the bounded area by horizontal summation and the bounded area by vertical summation is
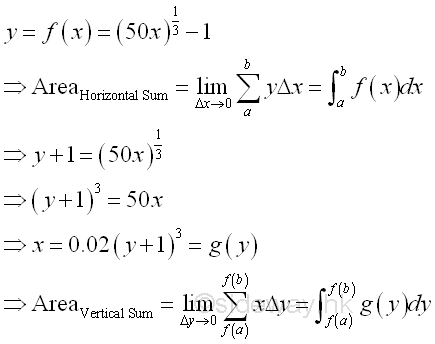
There is only a direct relationship between function f(x) and function g(x). And there is no direct relatonship between the horizontally summed area and the vertically summed area. In order to simplify the task of finding the integral, a transformation of the bounded area calculation is needed. The bounded area transformation can be carried out by integration by parts through the transformation of variable of integration.
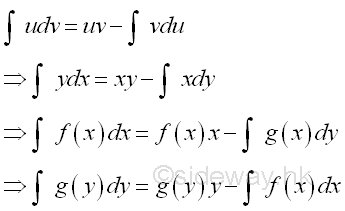
Geometrical Representation of Integration by Parts:
Through variable of integration transformation, the formula of integration by parts can be used for the transformation of bounded area summation.
In the formulas of integration by parts above, the x is obtained from dx through integration or the y is obtained from dy through integration. The practical forms of integration by parts are
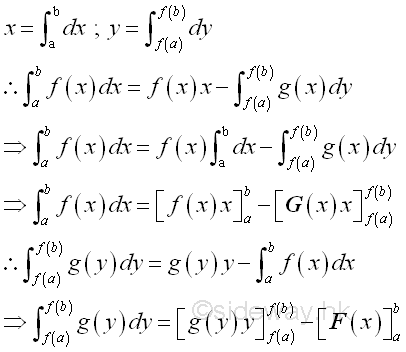
The first integral on the right hand side of the two integration by parts formulas above are equal because they are both derived from xy,
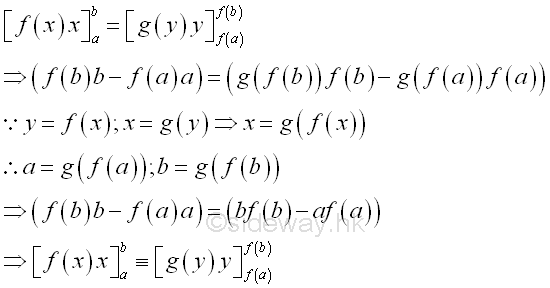
Therefore the term xy in the formula of integration by parts is equal to the product of the upper limits of x and y minus the product of the lower limits of x and y.
Geometrically, the relationship between the bounded area by horizontal summation and the bounded area by vertical summation is
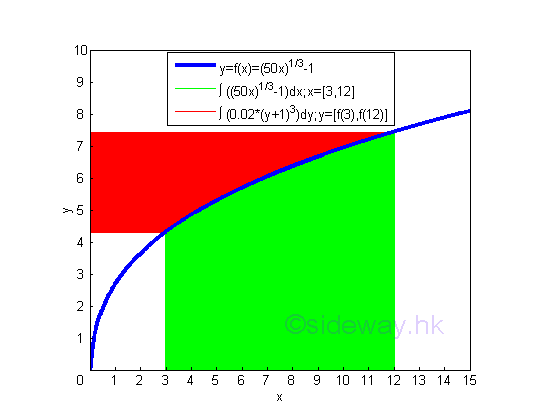
According to the graph, the sum of bounded red area and bounded green area is equal to the rectangular area formed by the upper limits (12,f(12)) and the origin (0,0) minus the rectangular area formed by the lower limits (3,f(3)) and the origin (0,0).
The bounded green area by horizontal summation is
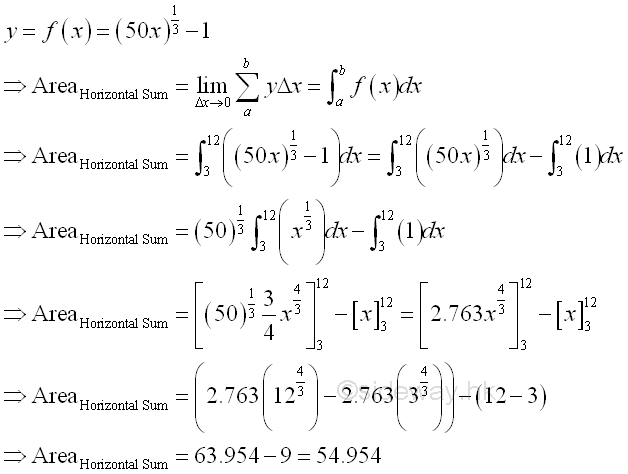
The bounded red area by vertical summation is
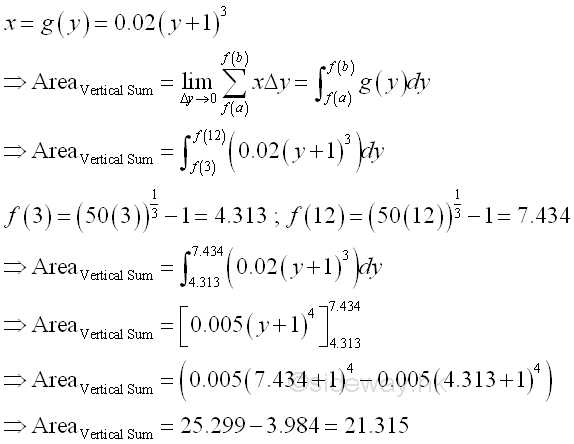
And the area formed by the two rectangular areas is
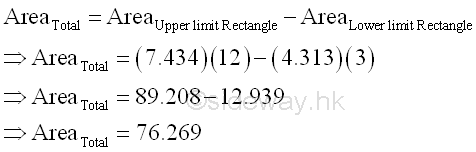
Therefore the term xy in the formula of integration by parts can be considered as the net total area of the net area of vertical sum plus the net area of horizontal sum, imply.
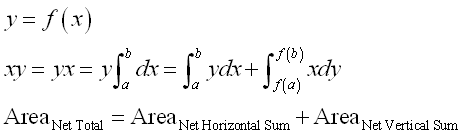
©sideway
ID: 111100004 Last Updated: 11/21/2011 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)
- Tefal BL83SD PerfectMix Cook Blender(last updated On 11/25/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/24/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/23/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/22/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
