Content
Internal Force in Cable
Cable with Discrete Concentrated Loads
Cable with Vertical Distributed Loads
Parabolic
Cable with Vertical Uniformly Distributed Loads
Catenary
Cable with Uniformly Distributed Axial Loads
Internal Force in Cable
Cable is flexable structure member used in structure for supporting transverse loads by the axial tension in cable. Although cable can be used to support concentrated load and distributed load, cable is normally used to carry distributed transverse loads, e.g. cable-stayed bridge.
Cable with Discrete Concentrated Loads
Cable is under discreter concentrated load when discrete loads are attached to the cable. By assuming the cable is inextensible and flexible, and the weight of the cable is negligble compared with the carried concentrated transverse load, cable segment between two successive concentrated loads can be considered as a two-force member similar to a truss member, but the internal force in a cable can only be tensile force along the cable.
Consider a cable AB with concentrated loads, C1, C2, and C3, the free body diagram is
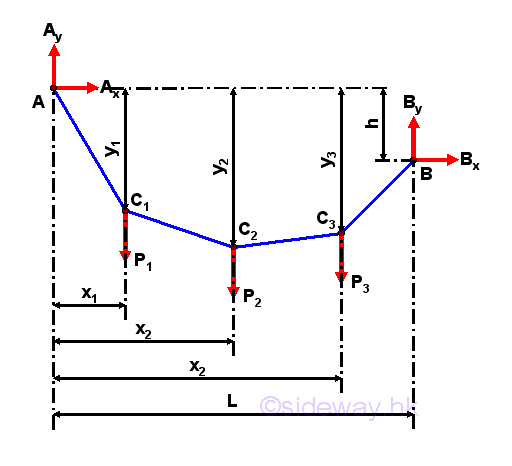
Equilibrium equations written from the free body diagram are.
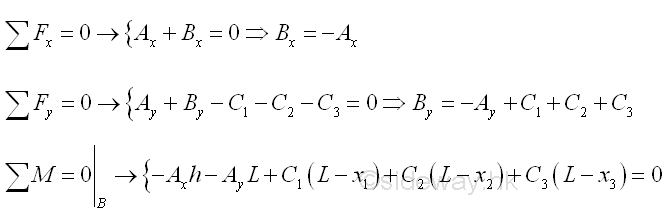
Since a cable structure is not a rigid body, the equilibrium equations are not sufficient for the determination of the four unknowns. However the shape of the cable can be stabilized by additional constraints, e.g. the cable is fixed at both ends and the location of load are fixed also. In general, the vertical load is balanced by the vertical components in cable segments, while the horizontal components in cable segments on the twe sides of the load are the additional constraints to stabled the location of the load. Therefore, when the cable structure is in equilibrium, more independent equilibrium equations can be derived from the loading points. For example, six independent equilibrium equations can be written from the three loading points, C1, C2, and C3, so two more unknowns, e.g. y1, and y2, can be determined beside the four unknown reactions on the supports. In other words, more information, e.g. the horizontal location of loading points, and the location of loading point C2 etc, is known
Since the cable structure is in equilibrium, two individual free body diagrams for the cable structure can be drawn by considering the whole cable is formed by two distinct rigid cable segments. Consider the free body diagram of the cable segment with A, C1, and C2 only,
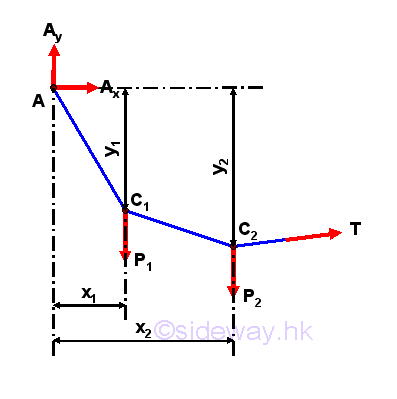
One more independent equilibrium equations can be written from the free body diagram by taking moment about C1,
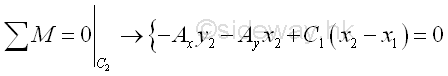
Therefore the four unknown Ax, Ay, Bx and By are
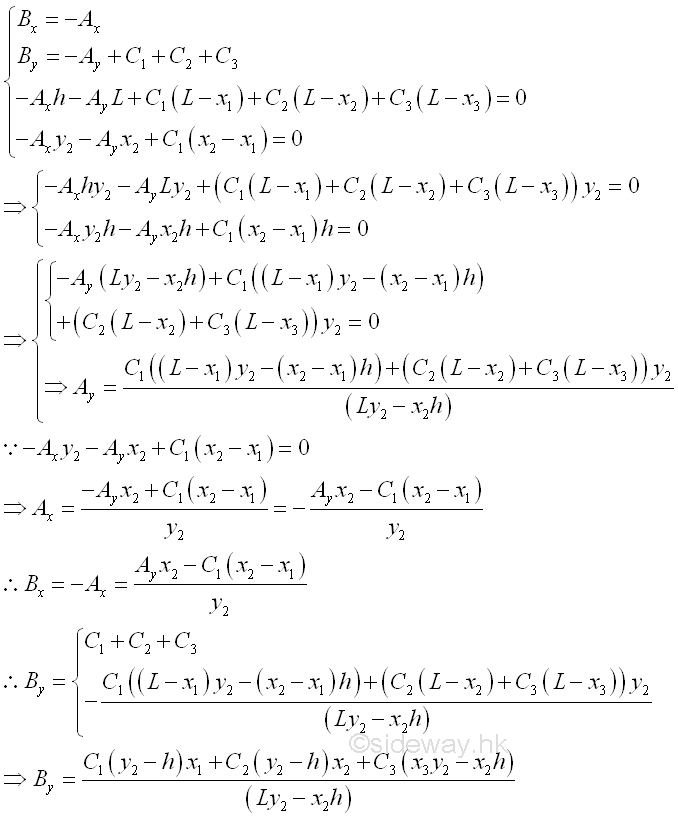
Magnitude of Tensions in cable segments AC1, and C3B are equal to the reaction force of supports A and B. Imply
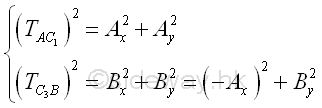
Because the tension in cable is always align with the axis of the cable, the height of loading points C1, and C3 can be determined by the slope of reaction force of supports A and B accordingly. Imply
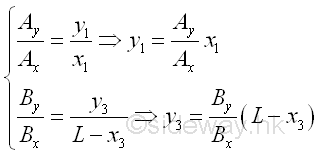
Cable with Vertical Distributed Loads
The cable is under vertical distributed loading, when an infinite number of concentrated loads are distributed along the cable. For example, the cable carries a vertical distributed load over the span L of the cable AB.
Consider a free body diagram of an infinitesimal cable element AB of length Gx under the vertical distributed load with vertical distributed load intensity w(x) per unit horizontal length. Assuming the tension difference between the ends of the infinitesimal cable element is ΔT. Assuming the vertical distributed load difference between the ends of the infinitesimal beam element is ΔW. Assuming the angle of tension difference between the ends of the infinitesimal beam element is Δθ. Imply
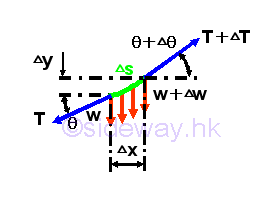
For an infinitesimal beam element, the vertical distributed load intensity over the the element can be considered as an uniformly distributed load over the element. Equilibrium equations written from the free body diagram are.
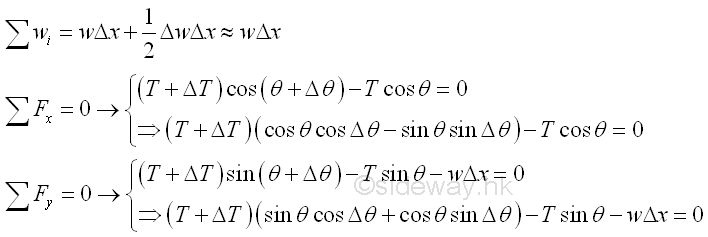
As Δx approaching zero, the equilibrium equations are approximately equals to.
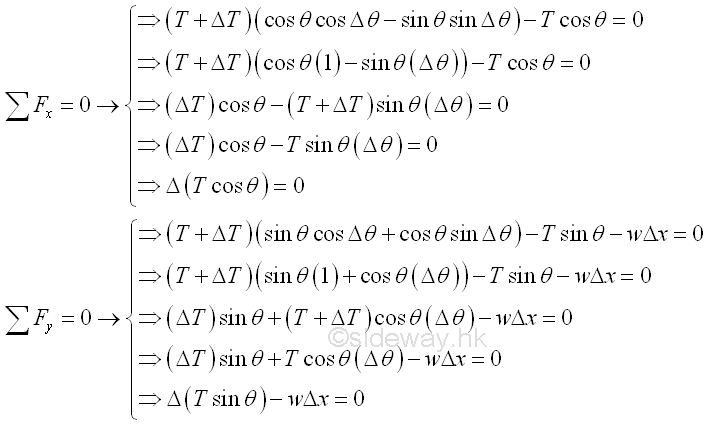
From the derived equation, the differential change of the horizontal component of the tension in the cable is zero, the horizontal component of the tension is a constant in the cable and therefore the vertical loads are carried by the vertical component of the tension only. Assume the horizontal component of the tension is equal to constant To. Both the tension T and angle θ are functions of x, since -1≤cosθ≤1 and the horizontal component of the tension in cable is a constant, the minimum tension, T is equal to To at the point where θ equals to zero. Imply
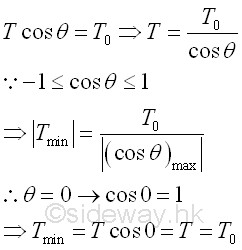
And when expressing the differential change of the vertical component of the tension in the cable in term of the constant horizontal component of tension To , since the tension in cable aligns with the axis of the cable, the differential change of angle θ.can also be expressed as the slope of tension in the cable. Imply
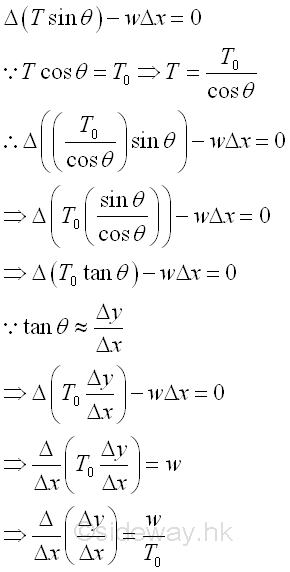
By taking the limit as the horizontal length Δx approaches zero. Imply
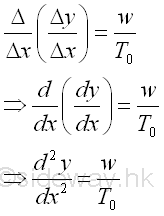
Therefore the shape of cable carrying a vertical distributed load can be determined by the governing differential equation about with the boundary conditions at the fixed ends of the cable. And the function of the shape of the cable is equal to y=f(x).
Similarly, the length of the cable can also be determined by
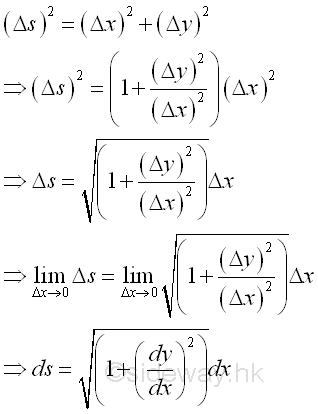
Parabolic Cable with Vertical Uniformly Distributed Loads
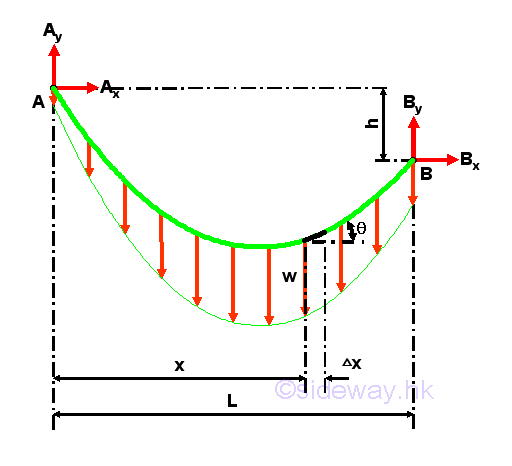
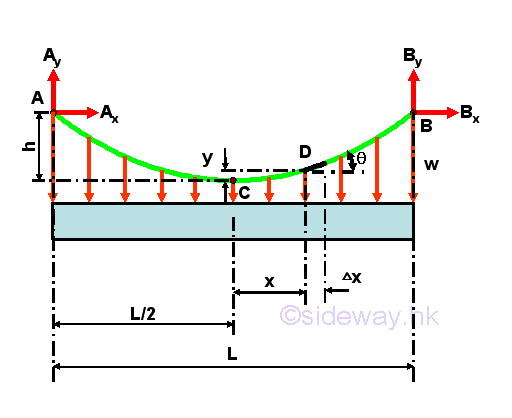
The cable is under vertical uniformly distributed loading, when a vertical load carried by the cable are evenly shared by a finite number of vertical concentrated supports along the horizonal distance of the cable. For example, the cable carries a vertical load distributed over the span L of the cable AB of same elevations with constant intensity w along the horizontal distance. Although the weight of the cable is not uniformly distributed along the horizontal distance because of the shape of the cable, the weight of the cable is usually much smaller than the carried load, and therefore the vertical loads acting on the cable can be assumed to be vertical uniformly distributed loads along the horizontal distance of the cable. The free body diagram of the cable with sag h is
According to the derived differential equation of cable with carried distributed load, the shape of the cable is depending on the horizontal intensity function w of the vertical load distributed. In other words, when an uniformly distributed load is assumed, the shape of the cable can also be determined by the differential equation of cable. Imply
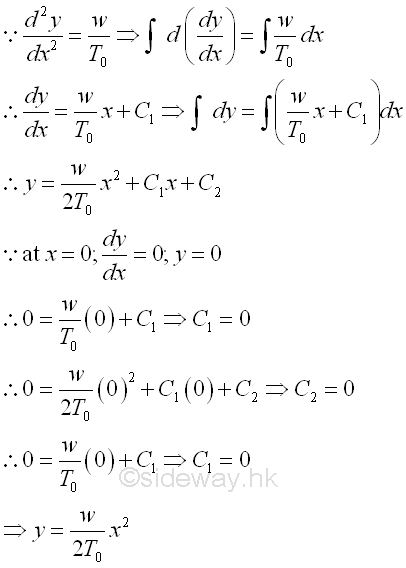
Therefore, the shape of the cable carrying uniformly distributed load along the horizontal distance is a vertical parabola. Considering the free body diagram of the cable segment CD,
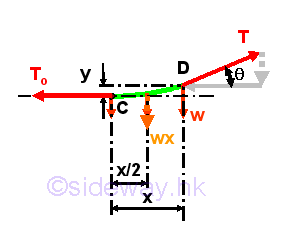
The equilibrium equation written from the free body diagram of the cable segment CD are,
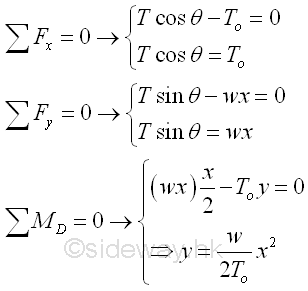
From the moment equilibrium equation, since the boundary conditions of cable AB, at x=±L/2, y=h, imply
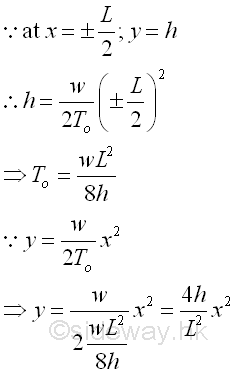
From the force equilibrium equations, since the three force vectors acting on the cable segment CD form a right angle triangle. imply
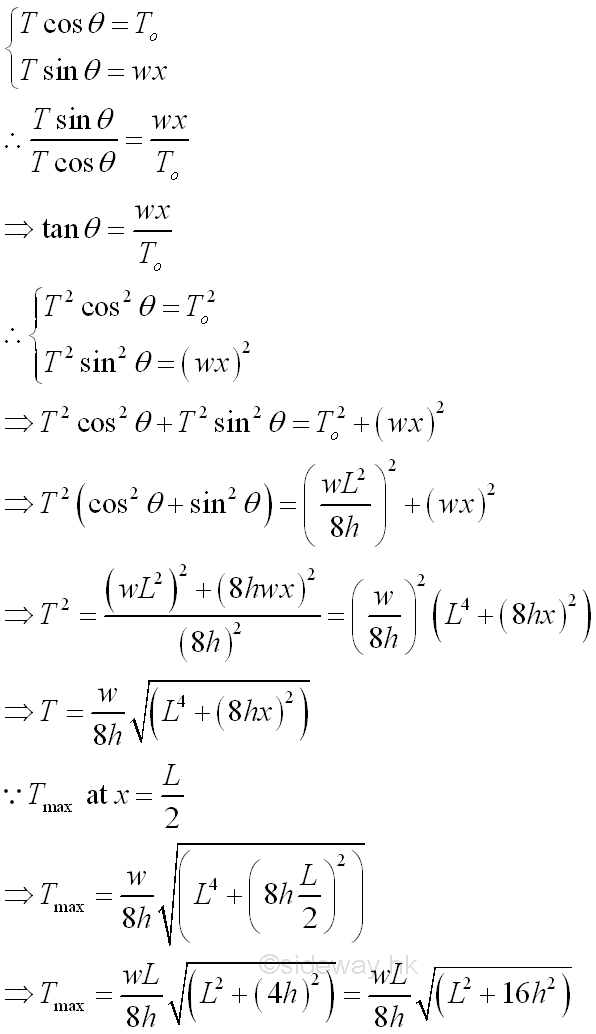
And the length of the cable AB can be determined by the curve length equation. imply

Since the value h/L is usually smaller than one, the series converges. If h is much smaller than L, the sum of series can be approximated by the first few terms of the series. Besides, if the cable is of different elevations, some of the described relations can only be applied to one side of the lowest point of the cable, and the other side of the cable should be determined separately according to the boundary conditions.
Catenary Cable with Uniformly Distributed Axial Loads
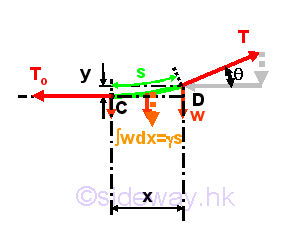
The cable is under uniformly distributed axial loading, when a vertical load carried by the cable are evenly distributed with a constant intensity along the axis of the cable itself. For example, the cable carries a vertical load distributed over the span L of the cable AB of same elevations with constant intensity ϒ along the axis of the cable itself. The load intensity ϒ is therefore equal to the load per unit length along the cable. And therefore when a cable carrying its own weight only, the weight of the cable is not uniformly distributed along the horizontal distance, as vertical distributed load is one of the variable in the governing differential equation of the cable, the shape of the cable will also be changed accordingly. The free body diagram of the cable with sag h is
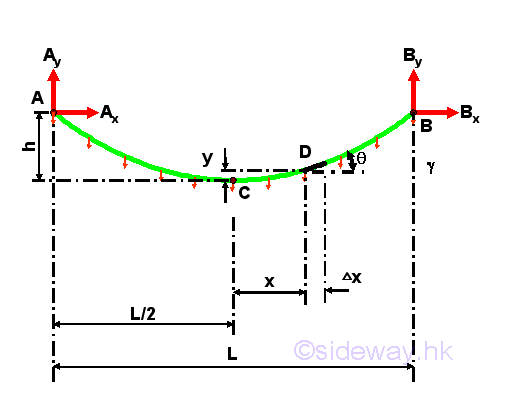
Consider a free body diagram of an infinitesimal cable element AB of length Gx under the vertical distributed load with uniform distributed load intensity ϒ per unit length of the cable itself. Assuming the tension difference between the ends of the infinitesimal cable element is ΔT. Assuming the vertical distributed load difference between the ends of the infinitesimal beam element is ΔW. Assuming the angle of tension difference between the ends of the infinitesimal beam element is Δθ. Imply

And the equilibrium equation written from the free body diagram of the infinitesimal beam element are
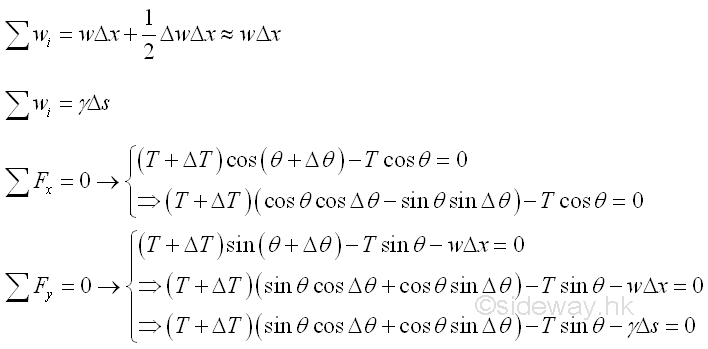
Therefore,
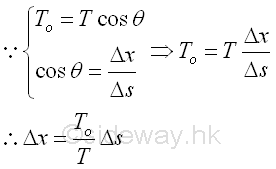
Similarly, by taking the limit as the horizontal length Δx approaches zero. Imply
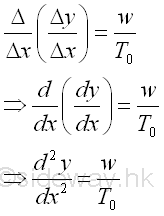
Since the vertical distributed load is with uniform distributed load intensity ϒ along the cable per unit length of the cable itself, the vertical distributed load w per unit horizontal distance is a function x also. Imply
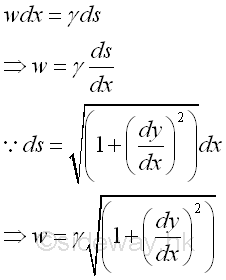
Therefore the governing differential equation of the cable can be expressed as
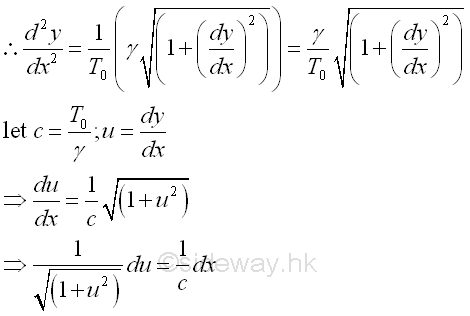
Considering the free body diagram of the cable segment CD,
The shape of the cable can be determined by integrating from point C to point D of the cable segment, Imply
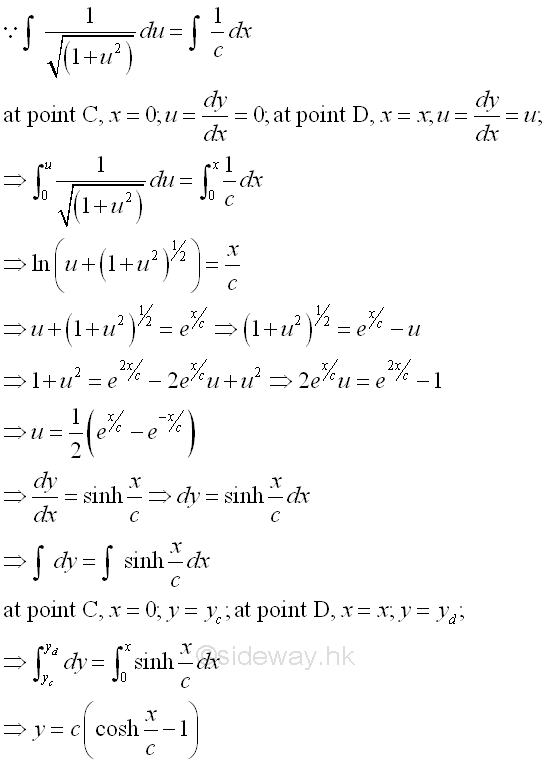
Therefore, the shape of the cable carrying uniformly distributed load along the cable, e.g. its own weight, is a vertical hyperbolic cosine curve with a distance c shifted downward. The cable is commonly called a catenary. The equation of the catenary can be reduced by setting the lowest point C of the cable segment CD to the constant c, and this non-zero lowest point C is then called the parameter of the catenary. Imply
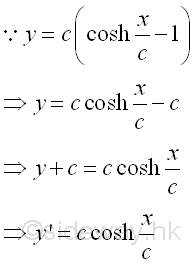
And the equilibrium equation written from the free body diagram of the cable segment CD are,
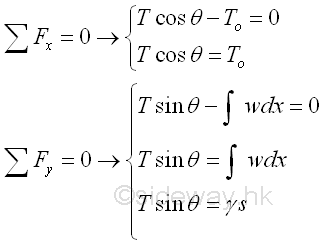
From the force equilibrium equations, since the three force vectors acting on the cable segment CD form a right angle triangle. imply
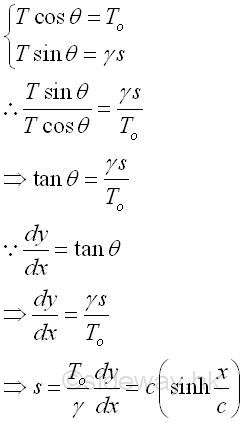
Since the three force vectors acting on the cable segment CD form a right angle triangle. Imply
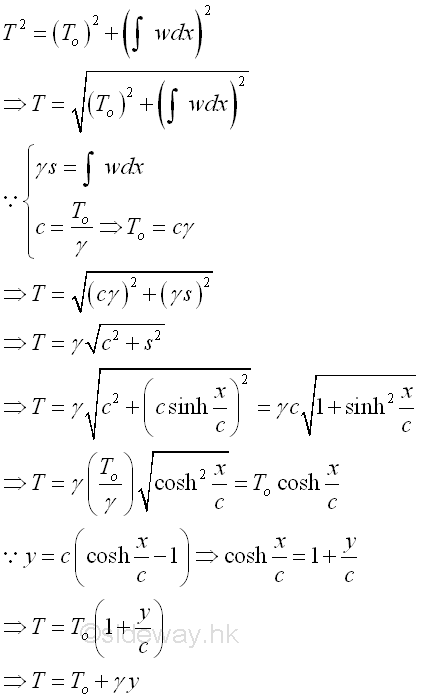
And the relation of length s of the cable and the horizontal distance x of cable segment CD can also be determined by
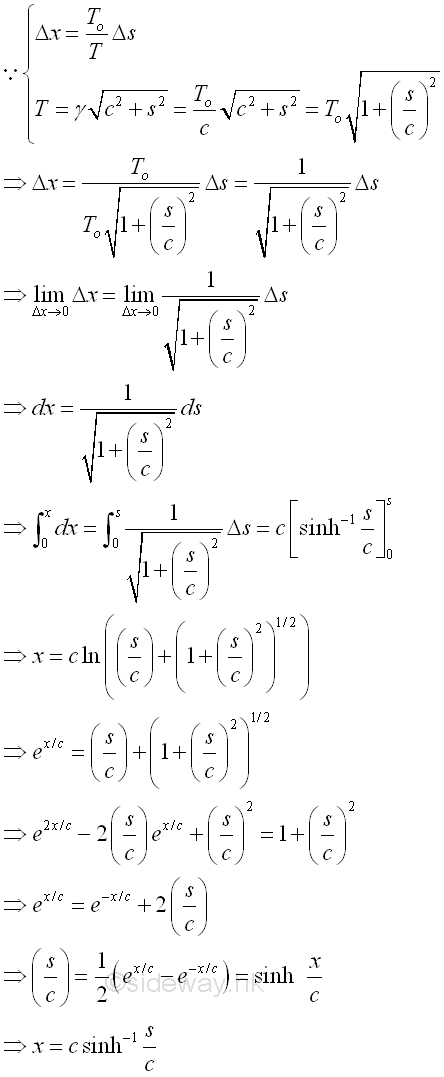
The relation between y and s is
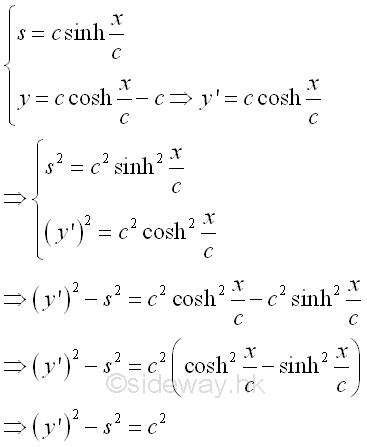
The relations between forces and the vertical load intensity along the cable are
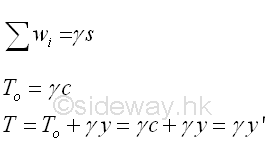
Similarly, if the cable is of different elevations, some of the described relations can only be applied to one side of the lowest point of the cable, and the other side of the cable should be determined separately according to the boundary conditions. The relation between vertical distance and sag h is
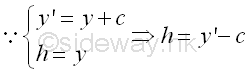
©sideway
ID: 120900011 Last Updated: 10/4/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/10/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 26![]()
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
