Content
Operations of Vectors
Algebraic Operations of Vectors
Scalar Multiplication of a Vector
Scalar Multiplication Rule
Addition of Two Vectors
Addition Rule
Vector Product Operation of Vectors
Dot Product of Two Vectors
Dot Product Rule
Cross Product of Two Vectors
Cross Product Rule
Operations of Vectors
The operations of vectors can be divided into algebraic operations and vector product operations.Algebraic Operations of Vectors
Like other mathematical calculations, rules are developed for the algebraic operations for vectorsScalar Multiplication of a Vector
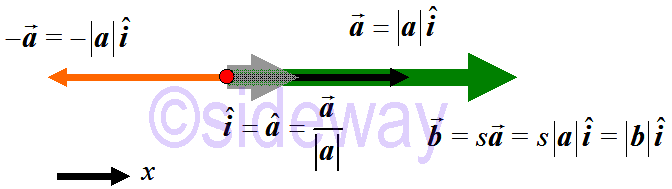 Consider a one-dimensional vector
Consider a one-dimensional vector 𝒂, a unit vector
𝒊can always be obtained such that vector
𝒂can be expressed in terms of the unit vector by multiplying a scalar quantity, the magnetude of the vector, that is
𝒂=|
𝒂|
𝒊. Therefore the scalar multiplication of a one-dimensional vector can be expressed as the multiplication of a scalar 𝑠 to the magnetude |
𝒂| of a vector
𝒂with respect to the unit vector
𝒂or
𝒊of the vector. That is 𝑠
𝒂=𝑠|
𝒂|
𝒊. And the negation of a vector always reverse the vector in opposite direction.
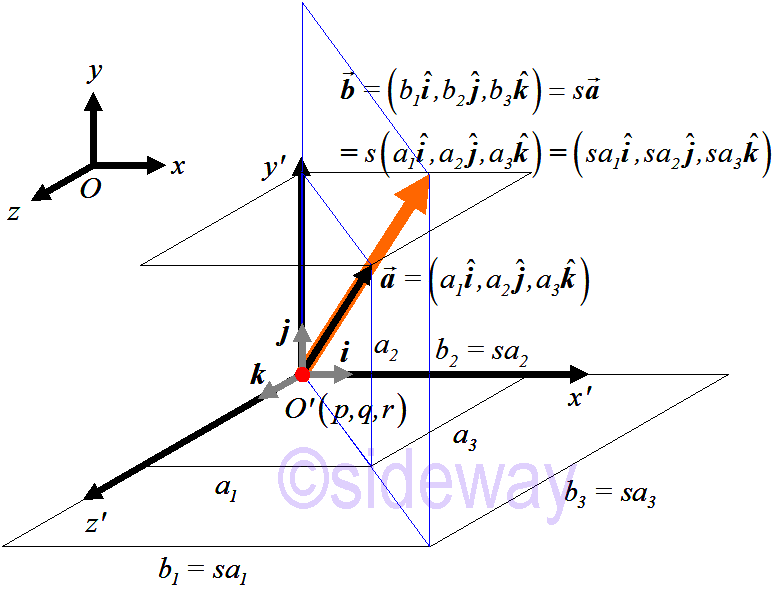
For a vector in space, the vector can be decomposited into components with respect to the rectangular Cartesian coordinate system. Each component of the vetor can be considered as one individual dimension. By the triangular approach, the scalar multiplication of a vector in space can also be expressed as the multiplication of a scalar to the magnetude of each component with respect to the unit vector accordingly. That is 𝑠𝒂
=𝑠(𝑎1,𝑎2,𝑎3)=(𝑠𝑎1,𝑠𝑎2,𝑠𝑎3)
Scalar Multiplication Rule
Scalar Multiplication of a VectorLet 𝒂
=(𝑎1,𝑎2,𝑎3) and 𝑠 be any real number
𝒃
=𝑠𝒂
=𝑠(𝑎1,𝑎2,𝑎3)=(𝑠𝑎1,𝑠𝑎2,𝑠𝑎3)=(𝑏1,𝑏2,𝑏3)
Addition of Two Vectors
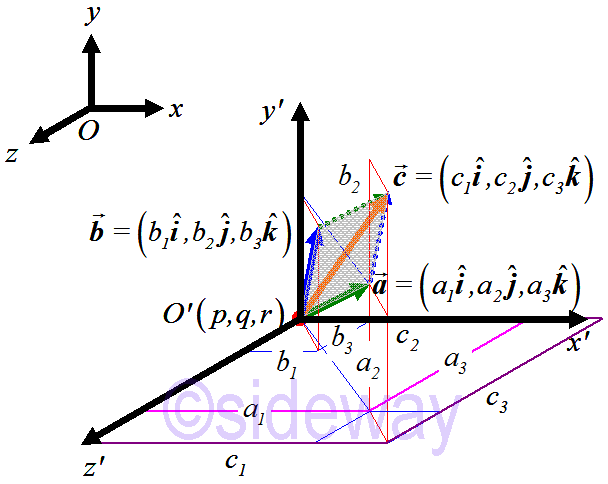 Geometrically, addition of two coinitial vectors, i.e.
Geometrically, addition of two coinitial vectors, i.e. 𝒂+
𝒃, can be visualized by using the parallelogram law through putting the initial point of second vector
𝒃at the terminal point of first vector
𝒂because two coinitial vectors are always coplanar vectors. The resultant vector
𝒄can be obtained by joining the initial point of first vector to the terminal point of second vector. That is
𝒄=
𝒂+
𝒃=(𝑎1,𝑎2,𝑎3)+(𝑏1,𝑏2,𝑏3)=(𝑎1+𝑏1,𝑎2+𝑏2,𝑎3+𝑏3)=(𝑐1,𝑐2,𝑐3)
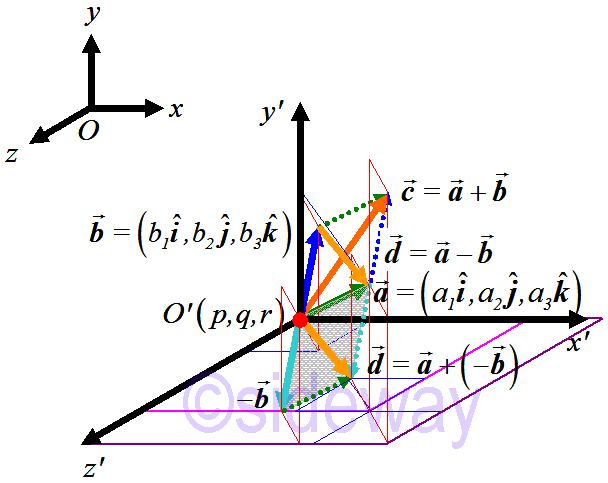 Similarly, subtraction of two coinitial vectors, i.e.
Similarly, subtraction of two coinitial vectors, i.e. 𝒂−
𝒃, can also be visualized by using the parallelogram law through putting the initial point of the negation of second vector
𝒃, i.e. −
𝒃, at the terminal point of first vector
𝒂. The resultant vector
𝒅can be obtained by joining the initial point of first vector to the terminal point of negation of second vector as in addition of vectors. That is
𝒅=
𝒂+(−
𝒃)
Besides, the subtraction of two coinitial vectors can be constructed directly from vectors
𝒂and
𝒃by the basic definition of vector, that is
𝒅=
𝒂−
𝒃=
𝐵𝐴=−
𝐴𝐵=−(
𝒃−
𝒂).
Addition Rule
Addition of VectorsLet 𝒂
=(𝑎1,𝑎2,𝑎3) and 𝒃
=(𝑏1,𝑏2,𝑏3) be coinitial vectors
𝒄
=𝒂
+𝒃
=(𝑎1,𝑎2,𝑎3)+(𝑏1,𝑏2,𝑏3)=(𝑎1+𝑏1,𝑎2+𝑏2,𝑎3+𝑏3)=(𝑐1,𝑐2,𝑐3)
Vector Product Operation of Vectors
Vector product operation of vectors are rules developed for specific product operation between two vectors. In general, the product of two vectors can be expressed as following.Let 𝒂
=(𝑎1𝒊,𝑎2𝒋,𝑎3𝒌), 𝒃
=(𝑏1𝒊,𝑏2𝒋,𝑏3𝒌)
𝒂
𝒃
=𝑎1𝒊𝑏1𝒊+𝑎1𝒊𝑏2𝒋+𝑎1𝒊𝑏3𝒌+𝑎2𝒋𝑏1𝒊+𝑎2𝒋𝑏2𝒋+𝑎2𝒋𝑏3𝒌+𝑎3𝒌𝑏1𝒊+𝑎3𝒌𝑏2𝒋+𝑎3𝒌𝑏3𝒌
𝒂
𝒃
=𝑎1𝑏1𝒊𝒊+𝑎2𝑏2𝒋𝒋+𝑎3𝑏3𝒌𝒌+𝑎1𝑏2𝒊𝒋+𝑎1𝑏3𝒊𝒌+𝑎2𝑏1𝒋𝒊+𝑎2𝑏3𝒋𝒌+𝑎3𝑏1𝒌𝒊+𝑎3𝑏2𝒌𝒋
𝒂
𝒃
=(𝑎1𝑏1𝒊𝒊+𝑎2𝑏2𝒋𝒋+𝑎3𝑏3𝒌𝒌)+(𝑎1𝑏2𝒊𝒋+𝑎2𝑏1𝒋𝒊+𝑎1𝑏3𝒊𝒌+𝑎3𝑏1𝒌𝒊+𝑎2𝑏3𝒋𝒌+𝑎3𝑏2𝒌𝒋)
Dot Product of Two Vectors
Dot product is commonly called scalar product because dot product of two vectors gives a scalar value along either vector. Dot product is also called inner product because dot product of two vectors is the sum of products of corresponding components of two vectors. The dot product operation of two vectors is developed to determine the along effect of one vector's component that along with another vector.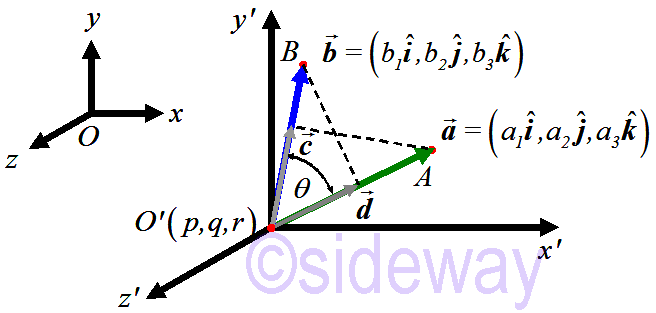 Therefore the dot product of two coinitial vectors,
Therefore the dot product of two coinitial vectors, 𝒂and
𝒃can be interpreted as the magnitude of one vector multiplies by the perpendicular projection of another vector on the previous one taken with the appropriate sign. In other words, the dot product between two vectors gives a scalar result with no direction.
According to the definition of dot product, the dot product of any unit vector dotted with itself is equal to 1, and the dot product magnetude of any two different unit vectors is equal to 0.
𝒊∙𝒊=𝒋∙𝒋=𝒌∙𝒌=𝟏
∙𝟏
=cos(0)𝟏
=𝟏
, undetermined, along either vector
𝒊∙𝒋=𝒌∙𝒊=𝒋∙𝒌=𝟏
∙𝟏
=cos(90)𝟏
=𝟎
𝒋∙𝒊=𝒊∙𝒌=𝒌∙𝒋=𝟏
∙𝟏
=cos(−90)𝟏
=𝟎
Let 𝒂
=(𝑎1𝒊,𝑎2𝒋,𝑎3𝒌), 𝒃
=(𝑏1𝒊,𝑏2𝒋,𝑏3𝒌)
𝒂
∙𝒃
=(𝑎1𝑏1𝒊∙𝒊+𝑎2𝑏2𝒋∙𝒋+𝑎3𝑏3𝒌∙𝒌)+(𝑎1𝑏2𝒊∙𝒋+𝑎2𝑏1𝒋∙𝒊+𝑎1𝑏3𝒊∙𝒌+𝑎3𝑏1𝒌∙𝒊+𝑎2𝑏3𝒋∙𝒌+𝑎3𝑏2𝒌∙𝒋)
⇒𝒂
∙𝒃
=𝑎1𝑏1𝒊∙𝒊+𝑎2𝑏2𝒋∙𝒋+𝑎3𝑏3𝒌∙𝒌
⇒𝒂
∙𝒃
=𝑎1𝑏1+𝑎2𝑏2+𝑎3𝑏3, undetermined along either vector
The dot product can be visualized geometrically in two-dimensional space.
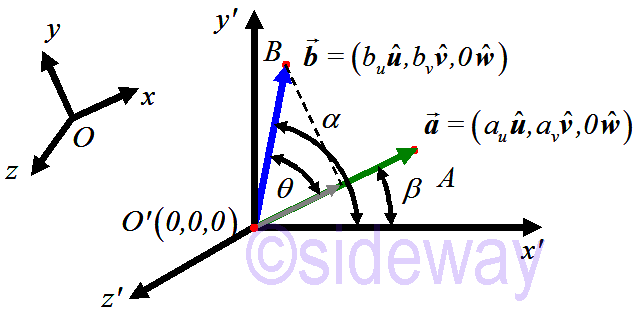 Select another rectangular Cartesian coordinate system such that vectors
Select another rectangular Cartesian coordinate system such that vectors 𝒂and
𝒃lie on the 𝑥𝑦-plane. The angles difference identity for cosine can then be used to derived the dot product of two vectors. And can further be extended to three-dimentional space.
Let 𝒂
=(𝑎𝑢𝒖,𝑎𝒗𝒗,𝑎𝑤𝒘)=(𝑎𝑢𝒖,𝑎𝒗𝒗,0𝒘), 𝒃
=(𝑏𝑢𝒖,𝑏𝑣𝒗,𝑏𝑤𝒘)=(𝑏𝑢𝒖,𝑏𝑣𝒗,0𝒘)
𝒂
=|𝒂
|𝒂
, 𝒃
=|𝒃
|𝒃
, 𝒂
∙𝒃
=|𝒃
|cos 𝜃 𝒂
, 𝒃
∙𝒂
=|𝒂
|cos 𝜃 𝒃
𝒂
∙𝒃
=|𝒂
|𝒂
∙𝒃
=|𝒂
||𝒃
|cos 𝜃 𝒂
𝒃
∙𝒂
=|𝒃
|𝒃
∙𝒂
=|𝒃
||𝒂
|cos−𝜃 𝒃
=|𝒃
||𝒂
|cos 𝜃 𝒃
⇒undetermined mathematically, either along 𝒂
or 𝒃
in direction
⇒𝒂
∙𝒃
=𝒃
∙𝒂
=|𝒂
||𝒃
|cos 𝜃=|𝒂
||𝒃
|(cos 𝛼 cos 𝛽+sin 𝛼 sin 𝛽)=|𝒂
||𝒃
|𝑏𝑢|𝒃
|𝑎𝑢|𝒂
|+𝑏𝒗|𝒃
|𝑎𝒗|𝒃
|𝒂
∙𝒃
=𝑎𝑢𝑏𝑢+𝑎𝑣𝑏𝑣 (direction in either 𝒂
or 𝒃
)
Value of dot product can be verified trigonometrically by applying the law of cosine to the triangle ⧍𝑂𝐴𝐵 with 𝜃 is the angle between vectors 𝒂and
𝒃.
Let 𝑂𝐴
=𝒂
=(𝑎1,𝑎2,𝑎3), 𝑂𝐵
=𝒃
=(𝑏1,𝑏2,𝑏3)
⇒|𝐴𝐵
|2=(𝑏1−𝑎1)2+(𝑏2−𝑎2)2+(𝑏3−𝑎3)2=|𝐵𝐴
|2=(𝑎1−𝑏1)2+(𝑎2−𝑏2)2+(𝑎3−𝑏3)2
⇒|𝐴𝐵
|2=|𝒂
|2+|𝒃
|2−2|𝒂
||𝒃
|cos 𝜃; law of cosine
⇒(𝑏1−𝑎1)2+(𝑏2−𝑎2)2+(𝑏3−𝑎3)2=(𝑎21+𝑎22+𝑎23)+(𝑎21+𝑎22+𝑎23)−2|𝒂
||𝒃
|cos 𝜃
⇒−2𝑎1𝑏1−2𝑎2𝑏2−2𝑎3𝑏3=−2|𝒂
||𝒃
|cos 𝜃
⇒|𝒂
||𝒃
|cos 𝜃=𝑎1𝑏1+𝑎2𝑏2+𝑎3𝑏3
⇒𝒂
∙𝒃
=|𝒂
||𝒃
|cos 𝜃=𝑎1𝑏1+𝑎2𝑏2+𝑎3𝑏3
Therefore angle between two coinitial vectors can be determined by dot product
|𝒂
||𝒃
|cos 𝜃=𝑎1𝑏1+𝑎2𝑏2+𝑎3𝑏3
⇒cos 𝜃=𝑎1𝑏1+𝑎2𝑏2+𝑎3𝑏3|𝒂
||𝒃
|
⇒𝜃=cos−1𝑎1𝑏1+𝑎2𝑏2+𝑎3𝑏3|𝒂
||𝒃
|
Dot Product Rule
Dot Product RuleLet 𝒂
=(𝑎1,𝑎2,𝑎3) and 𝒃
=(𝑏1,𝑏2,𝑏3) be coinitial vectors
𝒂
∙𝒃
=|𝒂
||𝒃
|cos 𝜃=𝑎1𝑏1+𝑎2𝑏2+𝑎3𝑏3
Cross Product of Two Vectors
Unlike determining the effect of one vector's component that along with another vector by the dot product opereation of two vector, the cross product operation of two vectors is developed to determine the cross effect of one vector's component that perpendicular to another vector. Therefore the axis of cross effect due to the cross product always normal to the plane of the two vectors lying in.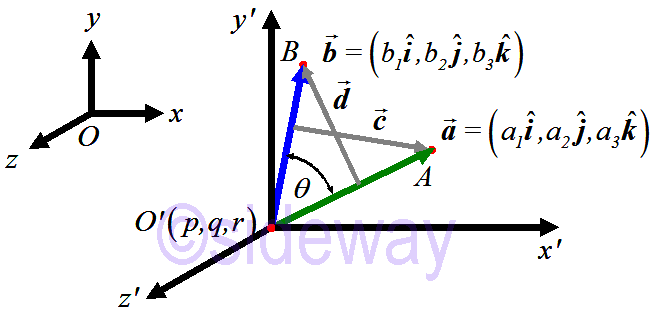 According to the definition of cross product, the cross product of any unit vector crossed with itself is equal to 𝟎. The cross product of any two different unit vectors that follows the right hand rule is equal to 𝟏normal, while the cross product of any two different unit vectors that does not follows the right hand rule is equal to −𝟏normal.
According to the definition of cross product, the cross product of any unit vector crossed with itself is equal to 𝟎. The cross product of any two different unit vectors that follows the right hand rule is equal to 𝟏normal, while the cross product of any two different unit vectors that does not follows the right hand rule is equal to −𝟏normal.
𝒊×𝒊=𝒋×𝒋=𝒌×𝒌=𝟏
×𝟏
=sin(0)𝟏
normal=𝟎
𝒊×𝒋=𝒋×𝒌=𝒌×𝒊=𝟏
×𝟏
=sin(90)𝟏
normal=𝟏
normal
⇒𝒊×𝒋=𝒌, 𝒋×𝒌=𝒊, 𝒌×𝒊=𝒋
𝒋×𝒊=𝒌×𝒋=𝒊×𝒌=𝟏
×𝟏
=sin(−90)𝟏
normal=−𝟏
normal=−(𝒊×𝒋)=−(𝒋×𝒌)=−(𝒌×𝒊)
⇒𝒋×𝒊=−𝒌, 𝒌×𝒋=−𝒊, 𝒊×𝒌=−𝒋
Let 𝒂
=(𝑎1𝒊,𝑎2𝒋,𝑎3𝒌), 𝒃
=(𝑏1𝒊,𝑏2𝒋,𝑏3𝒌)
𝒂
×𝒃
=(𝑎1𝑏1𝒊×𝒊+𝑎2𝑏2𝒋×𝒋+𝑎3𝑏3𝒌×𝒌)+(𝑎1𝑏2𝒊×𝒋+𝑎2𝑏1𝒋∙𝒊+𝑎1𝑏3𝒊×𝒌+𝑎3𝑏1𝒌×𝒊+𝑎2𝑏3𝒋×𝒌+𝑎3𝑏2𝒌×𝒋)
⇒𝒂
×𝒃
=(𝑎1𝑏1𝒊×𝒊+𝑎2𝑏2𝒋×𝒋+𝑎3𝑏3𝒌×𝒌)+((𝑎1𝑏2−𝑎2𝑏1)𝒊×𝒋+(𝑎2𝑏3−𝑎3𝑏2)𝒋×𝒌+(𝑎3𝑏1−𝑎1𝑏3)𝒌×𝒊)
⇒𝒂
×𝒃
=(𝑎2𝑏3−𝑎3𝑏2)𝒊+(𝑎3𝑏1−𝑎1𝑏3)𝒋+(𝑎1𝑏2−𝑎2𝑏1)𝒌
⇒𝒂
×𝒃
=𝒊 𝒋 𝒌𝑎1 𝑎2 𝑎3𝑏1 𝑏2 𝑏3
𝒊 𝒋𝑎1 𝑎2𝑏1 𝑏2
, determinant form:
↘ multiplication gives +value;
↙ multiplication gives −value
Magnetude of cross product can be considered geometrically as the area of a parallelogram with 𝜃 is the angle between vectors 𝒂and
𝒃.
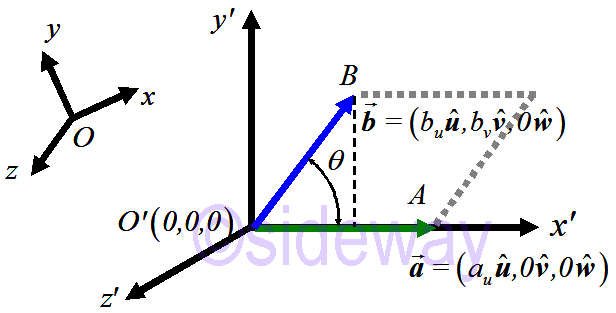 Select another rectangular Cartesian coordinate system such that vectors
Select another rectangular Cartesian coordinate system such that vectors 𝒂and
𝒃lie on the 𝑥𝑦-plane and vector
𝒂lies on the 𝑥-axis.
Let 𝒂
=(𝑎𝑢𝒖,𝑎𝒗𝒗,𝑎𝑤𝒘)=(𝑎𝑢𝒖,0𝒗,0𝒘), 𝒃
=(𝑏𝑢𝒖,𝑏𝑣𝒗,𝑏𝑤𝒘)=(𝑏𝑢𝒖,𝑏𝑣𝒗,0𝒘)
𝒂
×𝒃
=(𝑎𝒗𝑏𝑤−𝑎𝑤𝑏𝒗)𝒖+(𝑎𝑤𝑏𝑢−𝑎𝑢𝑏𝑤)𝒗+(𝑎𝑢𝑏𝒗−𝑎𝒗𝑏𝑢)𝒘
⇒|𝒂
×𝒃
|2=(𝒂
×𝒃
)∙(𝒂
×𝒃
)=(𝑎𝒗𝑏𝑤−𝑎𝑤𝑏𝒗)2+(𝑎𝑤𝑏𝑢−𝑎𝑢𝑏𝑤)2+𝑎𝑢𝑏𝒗−𝑎𝒗𝑏𝑢)2
⇒|𝒂
×𝒃
|2=(𝑎𝒗𝑏𝑤)2−2(𝑎𝒗𝑏𝑤𝑎𝑤𝑏𝒗)+(𝑎𝑤𝑏𝒗)2+(𝑎𝑤𝑏𝑢)2−2(𝑎𝑤𝑏𝑢𝑎𝑢𝑏𝑤)+(𝑎𝑢𝑏𝑤)2
+(𝑎𝑢𝑏𝒗)2−2(𝑎𝑢𝑏𝒗𝑎𝒗𝑏𝑢)+(𝑎𝒗𝑏𝑢)2
⇒|𝒂
×𝒃
|2=(𝑎𝑢𝑏𝒗)2, substitute values
⇒|𝒂
×𝒃
|=𝑎𝑢𝑏𝒗
∵|𝒂
|=𝑎𝑢, |𝒃
|sin 𝜃=𝑏𝑣
⇒|𝒂
×𝒃
|=|𝒂
||𝒃
|sin 𝜃=area of parallelogram
Therefore angle between two coinitial vectors can be determined by cross product.
|𝒂
||𝒃
|sin 𝜃=((𝑎2𝑏3−𝑎3𝑏2)2+(𝑎3𝑏1−𝑎1𝑏3)2+(𝑎1𝑏2−𝑎2𝑏1)2)
⇒sin 𝜃=((𝑎2𝑏3−𝑎3𝑏2)2+(𝑎3𝑏1−𝑎1𝑏3)2+(𝑎1𝑏2−𝑎2𝑏1)2)|𝒂
||𝒃
|sin−1((𝑎2𝑏3−𝑎3𝑏2)2+(𝑎3𝑏1−𝑎1𝑏3)2+(𝑎1𝑏2−𝑎2𝑏1)2)|𝒂
||𝒃
|
Cross Product Rule
Cross Product RuleLet 𝒂
=(𝑎1,𝑎2,𝑎3) and 𝒃
=(𝑏1,𝑏2,𝑏3) be coinitial vectors
𝒂
×𝒃
=|𝒂
||𝒃
|sin 𝜃=(𝑎2𝑏3−𝑎3𝑏2)𝒊+(𝑎3𝑏1−𝑎1𝑏3)𝒋+(𝑎1𝑏2−𝑎2𝑏1)𝒌
©sideway
ID: 130800175 Last Updated: 12/11/2019 Revision: 1 Ref:
References
- Robert C. Wrede, 2013, Introduction to Vector and Tensor Analysis
- Daniel Fleisch, 2012, A Student’s Guide to Vectors and Tensors
- Howard Anton, Chris Rorres, 2010, Elementary Linear Algebra: Applications Version
Latest Updated Links
- Ikea SANDSBERG table(last updated On 11/4/2025)
- Ikea TISKEN toilet roll holder(last updated On 11/3/2025)
- Philips CL400 Ceiling Light 36W(last updated On 11/2/2025)
- Philips CL400 Ceiling Light 24W(last updated On 11/1/2025)
- Philips CL400 Ceiling Light 13W(last updated On 10/30/2025)
- Ikea TISKEN basket(last updated On 10/29/2025)
- Ikea TISKEN towel rack(last updated On 10/28/2025)
- Ikea REXBEGONIA mattress protector(last updated On 10/27/2025)
- Ikea KEJSAROLVON mattress protector(last updated On 10/26/2025)
- Ikea KVARNVEN ergonomic pillow(last updated On 10/25/2025)
- Ikea BRUKSVARA pocket prung mattress(last updated On 10/24/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 27![]()
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
