Logarithm TheoremPythagorean TheoremCombinatoricsQuadratic EquationsSequence and SeriesLinear AlgebraDiophantine EquationElliptic CurveAlgebra Result
Draft for Information Only
Content
Vector Components
Components of Vector
One Dimension
Two Dimension
Three Dimension
Vector in Space
Vector Components
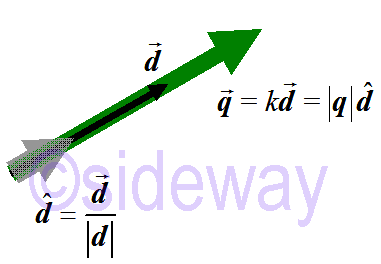 A vector is used to represent the magnitude and direction of a vector quantity. A vector quantity, 𝑄, is therefore can be expressed as a simple vector
A vector is used to represent the magnitude and direction of a vector quantity. A vector quantity, 𝑄, is therefore can be expressed as a simple vector 𝒒. Or in form of a scaled vector by simple geometry operation, that is a scalar 𝑘 times a directional vector
𝒅or the magnitude |𝒒| times a unit directional vector
𝒅. In other words, the study of vector components can only focus on the directional vector irrespective of its magnitude.
Components of Vector
In general, the values that are used to represent a vector are called the components of the vector, and the number of components used to define a vector is equal to the number of dimensions of interest.One Dimension
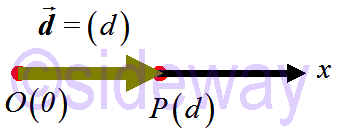 Since a one-dimensional vector always lies along a line, only one value is needed to specify the vector. There is only one component for a one-dimensional vector. For example,
Since a one-dimensional vector always lies along a line, only one value is needed to specify the vector. There is only one component for a one-dimensional vector. For example, 𝒅=(𝑑)
Two Dimension
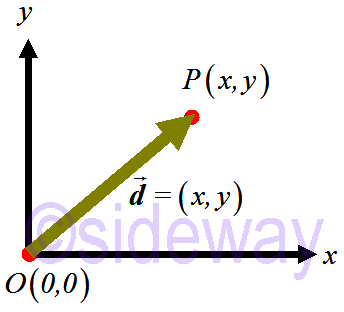 Since a two-dimensional vector always lies in a Cartesian plane, two values are needed to specify the vector. There are two components for a two-dimensional vector. For example,
Since a two-dimensional vector always lies in a Cartesian plane, two values are needed to specify the vector. There are two components for a two-dimensional vector. For example, 𝒅=(𝑥,𝑦).
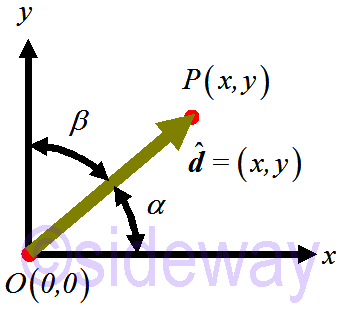 If
If 𝒅is a unit vector, the components of the vector can be expressed in terms of angles between the vector and coordinate axes, that is 𝑥=
𝒅=(
Since the components of a vector is an ordered set, the rectangular Cartesian coordinate system of components 𝑥 and 𝑦 must be arranged in correct order following the right-hand rule.
Three Dimension
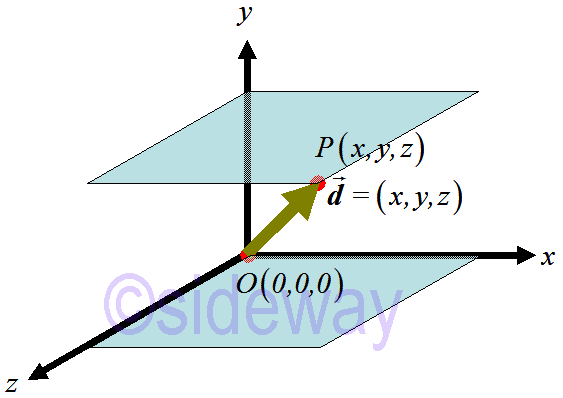 Since a three-dimensional vector always lies in a Cartesian space, three values are needed to specify the vector. There are three components for a three-dimensional vector. For example,
Since a three-dimensional vector always lies in a Cartesian space, three values are needed to specify the vector. There are three components for a three-dimensional vector. For example, 𝒅=(𝑥,𝑦,𝑧).
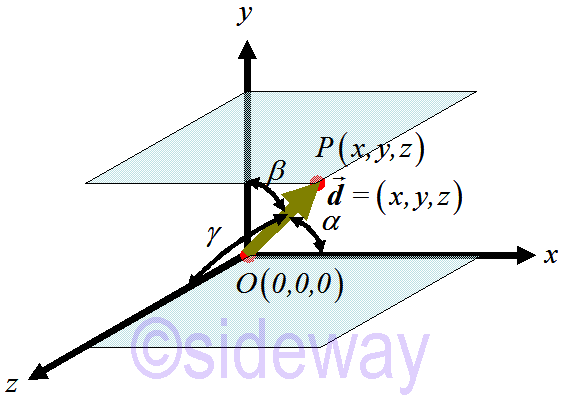 If
If 𝒅is a unit vector, the components of the vector can be expressed in terms of angles between the vector and coordinate axes, that is 𝑥=
𝒅=(
Since the components of a vector is an ordered set, the rectangular Cartesian coordinate system of components 𝑥, 𝑦, 𝑧 and must be arranged in correct order following the right-hand rule.
Vector in Space
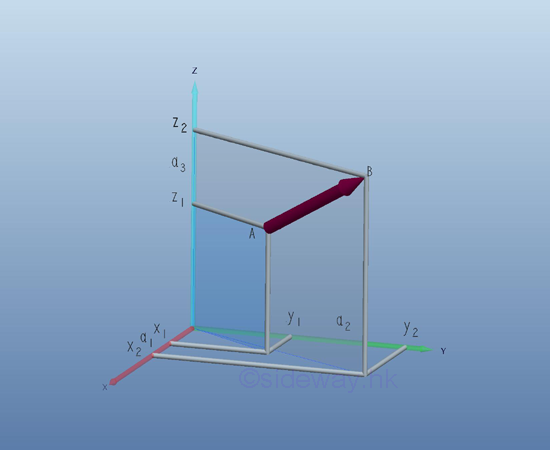 Since a point can be considered as a geometric object in a three dimensional
space, a point can be represented by the coordinates of a coordinate system such
that a vector can be expressed algebraically. The most common system for a three
dimensional space is the rectangular coordinate system called Cartesian coordinate
system with three mutually perpendicular straight axes of same scale. A vector
Since a point can be considered as a geometric object in a three dimensional
space, a point can be represented by the coordinates of a coordinate system such
that a vector can be expressed algebraically. The most common system for a three
dimensional space is the rectangular coordinate system called Cartesian coordinate
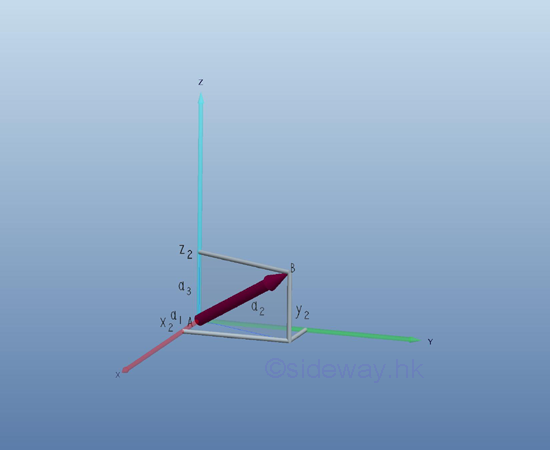
system with three mutually perpendicular straight axes of same scale. A vector 𝒂with initial point 𝐴 and terminal point 𝐵 can be expressed in term of coordinates 𝐴(𝑥1,𝑦1,𝑧1) and 𝐵(𝑥2,𝑦2,𝑧2). The vector
𝒂can also be interpreted as a displacement vector
𝐴𝐵displaced from point 𝐴 to point 𝐵. And the geometry of the directed line segment corresponding to the displacement vector can be specified by the numbers 𝑎1=𝑥2-𝑥1, 𝑎2=𝑦2-𝑦1, and 𝑎3=𝑧2-𝑧1 with respect to point 𝐴. These numbers are called components of the vector
𝒂with respect to the corresponding Cartesian coordinate system because vector
𝒂can be represented by these components. That is
𝒂
=𝐴𝐵
=(𝑥2-𝑥1,𝑦2-𝑦1,𝑧2-𝑧1)=(𝑎1,𝑎2,𝑎3)𝒂can be determined by the Pythagorean theorem geometrically.
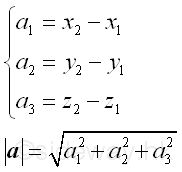 As the components 𝑎1, 𝑎2, and 𝑎3 of vector
As the components 𝑎1, 𝑎2, and 𝑎3 of vector 𝒂are derived from the end points of the vector by subtracting the coordinates of initial point from the coordinates of the terminal point, the components of vector are independent of the choice of the initial point of the vector and are dependent on the magnitude and direction of the vector only. In other words, the components of vector
𝒂is a free vector bounded to point 𝐴 with respect to the corresponding Cartesian coordinate system.
 Physically, a free vector can be translated arbitrarily to indicate a vector quantity
at a point having equal vector quantity. The terminal point of the vector
can be determined uniquely once the initial point of the vector is fixed. If the
initial point of a vector is located at the origin, the components of the vector
are then equal to the coordinate of the terminal point with respect to the corresponding Cartesian coordinate system. The vector with initial point bounded at the origin is called position vector. Therefore, any vector in three dimensional space can be
represented by a position vector by translating the initial point of the vector
to the origin. And for a specified Cartesian coordinate system, each vector
in space can be mapped to ordered triple components in one-to-one
relation with respect to the corresponding Cartesian coordinate system. In other words,
two vectors
Physically, a free vector can be translated arbitrarily to indicate a vector quantity
at a point having equal vector quantity. The terminal point of the vector
can be determined uniquely once the initial point of the vector is fixed. If the
initial point of a vector is located at the origin, the components of the vector
are then equal to the coordinate of the terminal point with respect to the corresponding Cartesian coordinate system. The vector with initial point bounded at the origin is called position vector. Therefore, any vector in three dimensional space can be
represented by a position vector by translating the initial point of the vector
to the origin. And for a specified Cartesian coordinate system, each vector
in space can be mapped to ordered triple components in one-to-one
relation with respect to the corresponding Cartesian coordinate system. In other words,
two vectors 𝒂and
𝒃are equal if and only if the corresponding component of two vectors are equal. That is 𝑎1=𝑏1, 𝑎2=𝑏2, and 𝑎3=𝑏3.
As both the magnitude and the direction of the directed line segment of the corresponding vector can be obtained from the components of the corresponding vector, the geometry of the directed line segment in three dimensional space can also be determined by the ordered triple components of the vector in one-to-one relation with respect to the corresponding Cartesian coordinate system.
However, the vector representation of quantity with magnitude and direction is always dependent on the choice of coordinate system.
©sideway
ID: 191201202 Last Updated: 12/12/2019 Revision: 0 Ref:
References
- Robert C. Wrede, 2013, Introduction to Vector and Tensor Analysis
- Daniel Fleisch, 2012, A Student’s Guide to Vectors and Tensors
- Howard Anton, Chris Rorres, 2010, Elementary Linear Algebra: Applications Version
Latest Updated Links
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 22
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
