Content

Acoustic Propagation

Consider a longitudinal sound wave traveling along a direction in a fluid, the acoustic disturbance propagation causes medium particle displacement in form of oscillation, and the medium particles return to its former state after the disturbance has passed.

The fluid in most common engineering acoustic system can be assumed as an idea gas, and obey the perfect gas law. That is

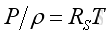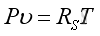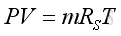or or or or

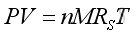
where

P is pressure
ρ is density of medium
R_s is specific gas constant of medium
T is absolute temperature
υ is specific volume
V is volumn of medium
m is mass of medium
n is mass of medium
R is universal gas constant
M is number of moles of medium

In equilibrium state, the perfect gas equation is still valid under the sound propagation process.

To simplify the problem, the fluid medium is assumed to be homogeneous and isotropic that properties of the medium are same everywhere. The medium is also assumed to be perfect elastic for the sound wave propagation with no energy loss. The fluid is also assumed as an inviscid fluid with no drag force. As the fluid medium is in equilibrium, the gravitational effects on sound propagation can also be neglected.

Since the acoustic oscillations are very small, the temperature gradients due to the oscillation is very small also. Nearly no heat can be transferred to other medium particle during the sound propagation process. Therefore the wave propagation process can be assumed to be adiabatic and reversible, an isentropic process. For adiabatic process, the relation of pressure and density is:

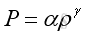or

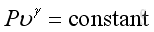
where

P is pressure
α is constant
γ is adiabatic index of medium
υ is specific volume

The relationship of pressure and density due to sound wave is non-linear, but this non-linearity effect is usually negligible when comparing with the sound perception of ear. When the fluctuations of medium particle are small, e.g. less than 100dB, the acoustic  properties can be assumed linear.

Acoustic Fluctuation

At initial equilibrium ambient state, the medium is assumed to be homogeneous and quiescent. The physical properties are independent of position and time. The initial medium velocity also equals to zero ( 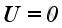) and the physical properties are defined as:

At the acoustic static, assuming there is no mass entering or leaving the system for the sound propagation, the acoustic disturbance will alter the physical properties of medium and can be defined as:

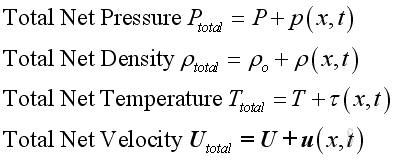
where

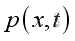is the acoustic pressure variations
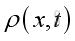is the acoustic density variations
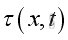is the acoustic temperature variations
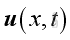is the acoustic velocity variations

The acoustic fluctuation is a function of traveling distance and time. The fluid returns to its former equilibrium state after the disturbance has passed.

Besides, the representation of corresponding volume or specific volume of medium are:

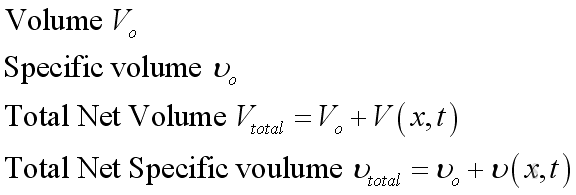
where

V_o is the initial volume of medium
υ_o is the initial specific volume of medium
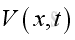is the acoustic volumetric variations
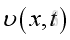is the acoustic specific volume variations