Content
Derivatives of Exponential and Logarithmic Functions
Constant e
Definition of e
Another
Definition of e
Define constant e as a sum of infinite series
Definition of
Natural Exponential Function
Derivatives of Exponential and Logarithmic Functions
Derivatives of Exponential and Logarithmic Functions
Both exponential and logarithmic functions are very important in real world problems. The natural exponential function ex has the base e. And the natural logarithmic function, ln(x) is the inverse of the natural exponential function. The constant e is an important constant in finding limits and derivatives also.
Constant e
The number e is base of the natural logarithm. The number e is a constant sometimes known as Napier's constant, named after the Scottish mathematician John Napier who introduced logarithms. The mathematical constant e is also called Euler number with its symbol honors Swiss mathematician Leonhard Euler.
The constant e is an irrational number. The numerical value of e to 10 decimal places is 2.7182818284.
Definition of e
There are many ways to define the mathematical constant e. The number e can be defined as the limit of:
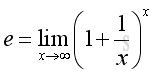
For x approaching +∞, there always exists a pair of integers such that:
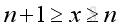
Imply:
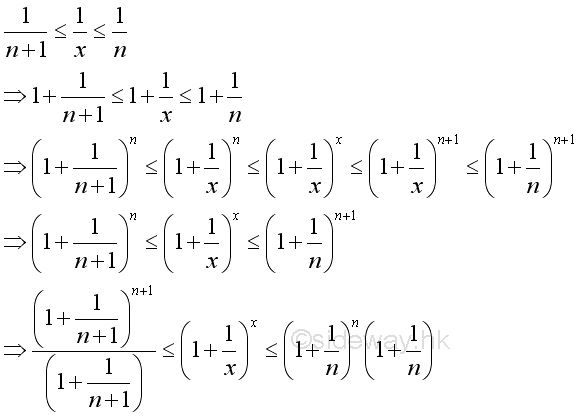
Since the following limits exist and are equal to 1:
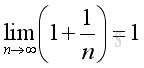 and
and
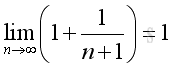
Imply:
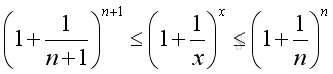
And if limits exist when n approaching +∞, that is:
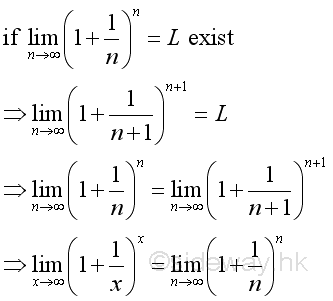
Therefore the limit when x approaching +∞ can be proved by the limit when integer n approaching +∞. And using Binomial Theorem to expand the terms in the bracket of the limit goes up to n, where n approaching +∞:
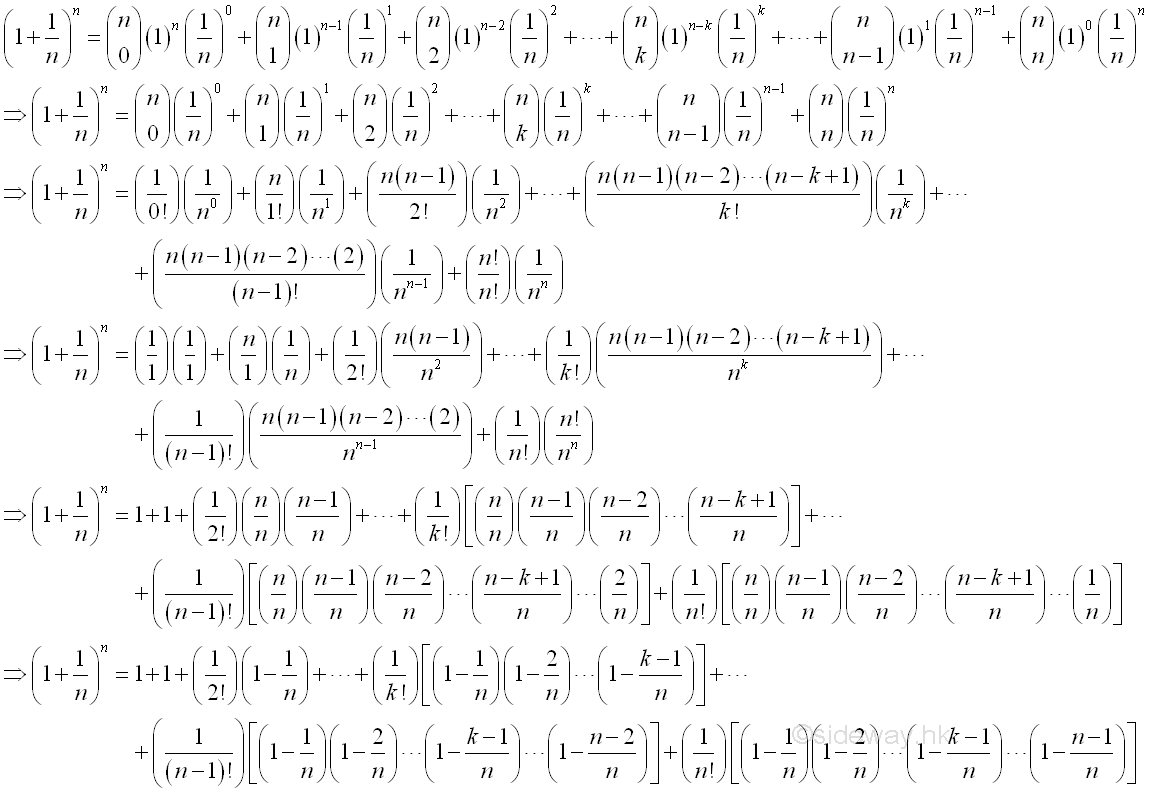
Therefore the limit when n approaching +∞ is:
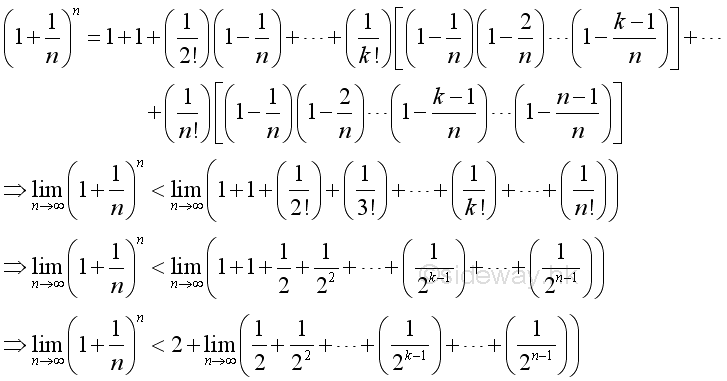
The limit on the RHS when n approaching +∞ is:
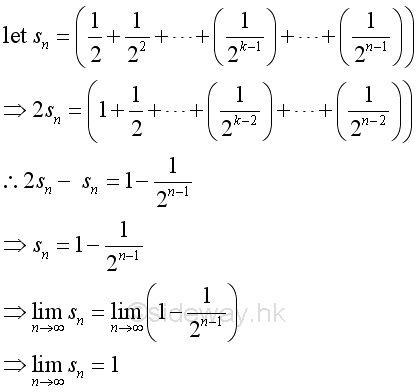
The limit on the LHS when n approaching +∞ exists:
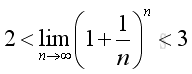
Therefore the limit of the series exists:
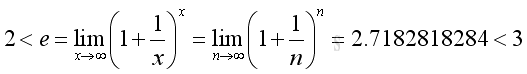
For x approaching -∞, let x=-y then:
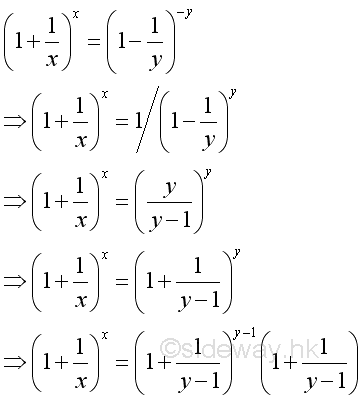
As shown before, when y approaching +∞, imply:
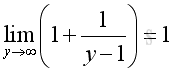 and
and
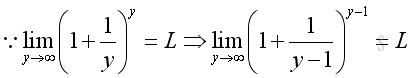
Therefore, when x approaching ∞, imply:
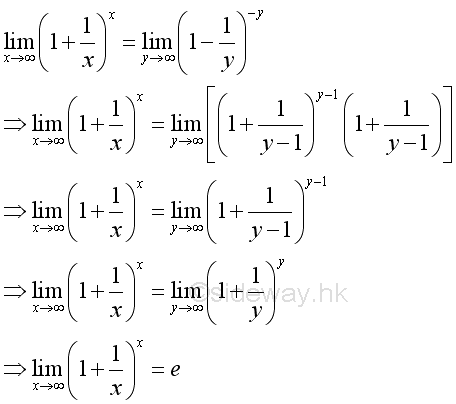
Another Definition of e
Similarly, the limit can be rewritten for x approaching 0, imply:
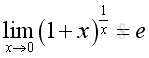
Define constant e as a sum of infinite series
Besides, as shown in the binomial expansion, the limit can also be expressed as:
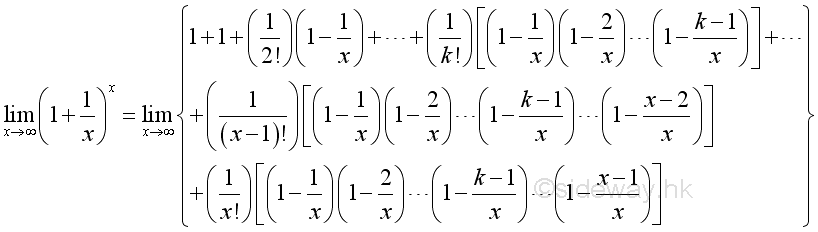
After rearrangement, imply:
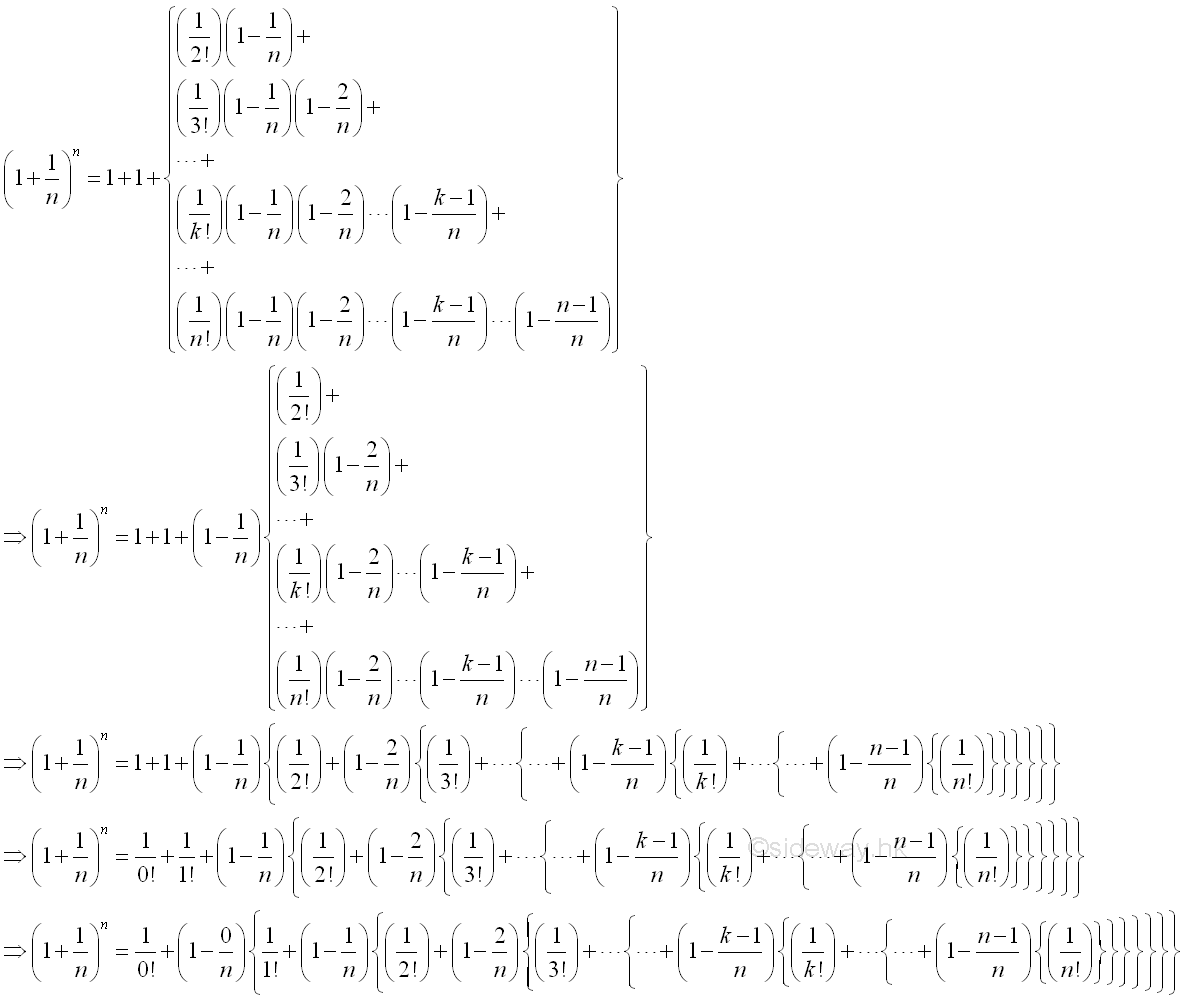
Consider the k term, when k=1:
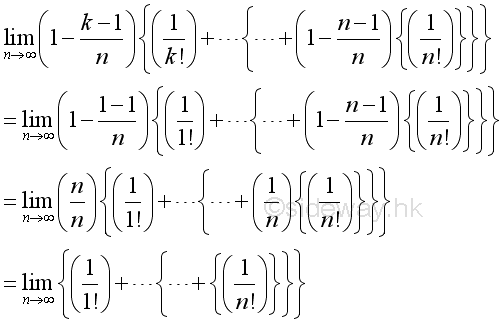
Consider the k term, when k=n-1:
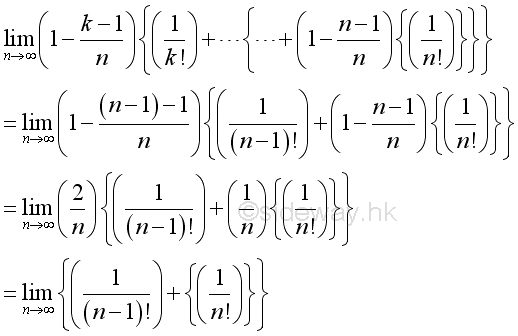
Therefore the numeric value of k term is bounded and since n approaching ∞, for every k there is a n term such that n>>k:
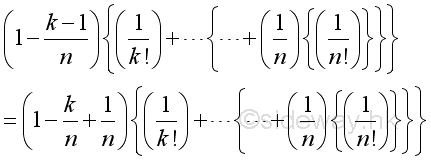
Imply when n approaching ∞, the limit of k term can be approximated by:
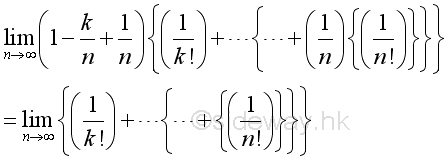
Therefore when x approaching ∞, the limit of can be approximated by:
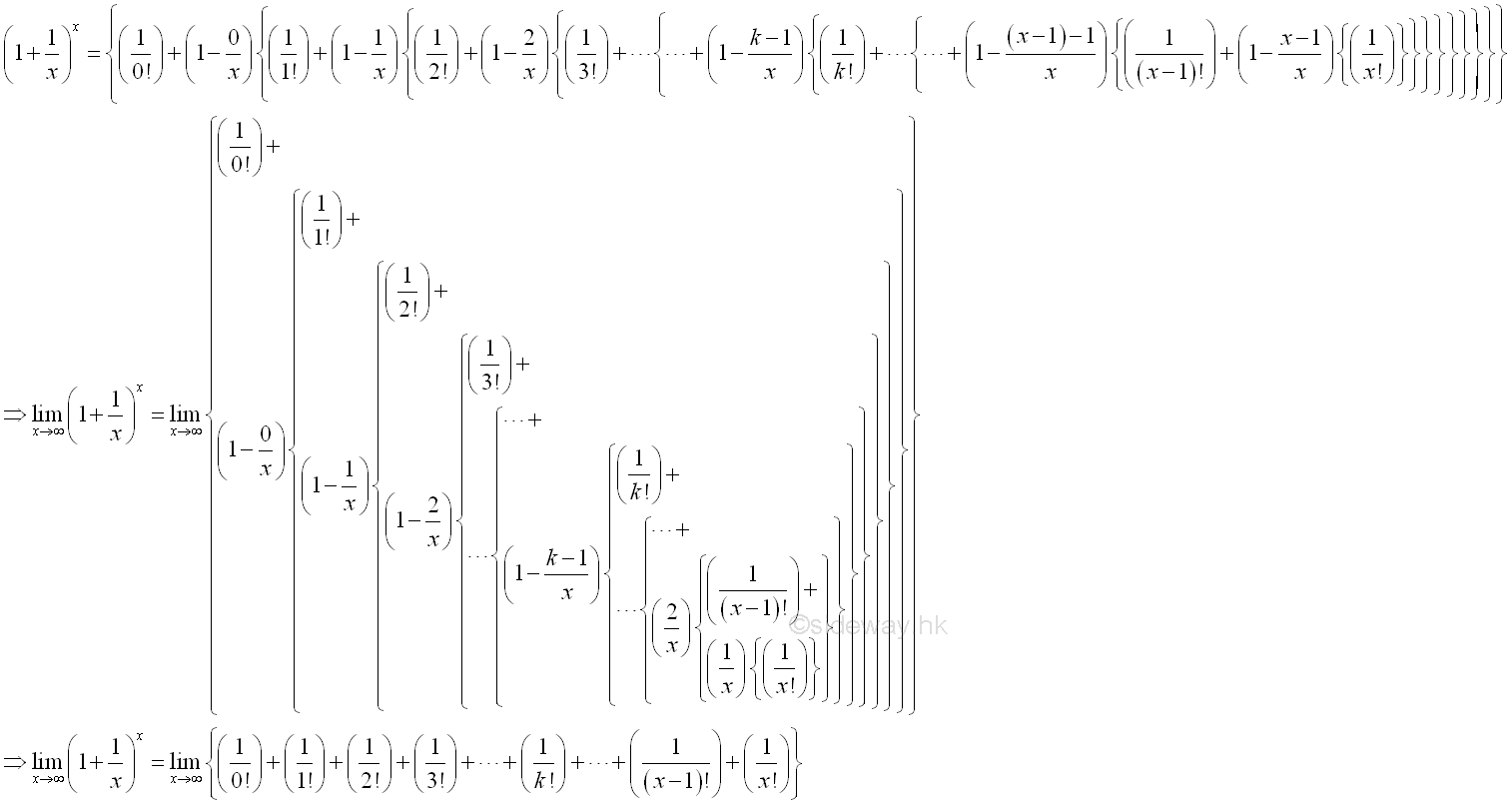
Imply:
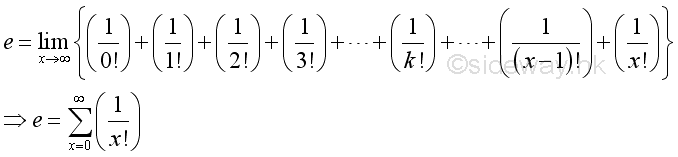
Definition of Natural Exponential Function
The Natural Exponential Function can be expressed as:
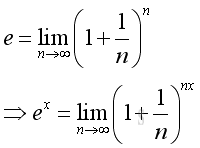
Let m=nx, since n approaching ∞, there must exist a numeric value such that m is an integer, imply:
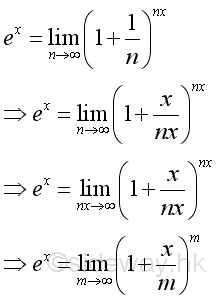
Using Binomial Theorem to expand:
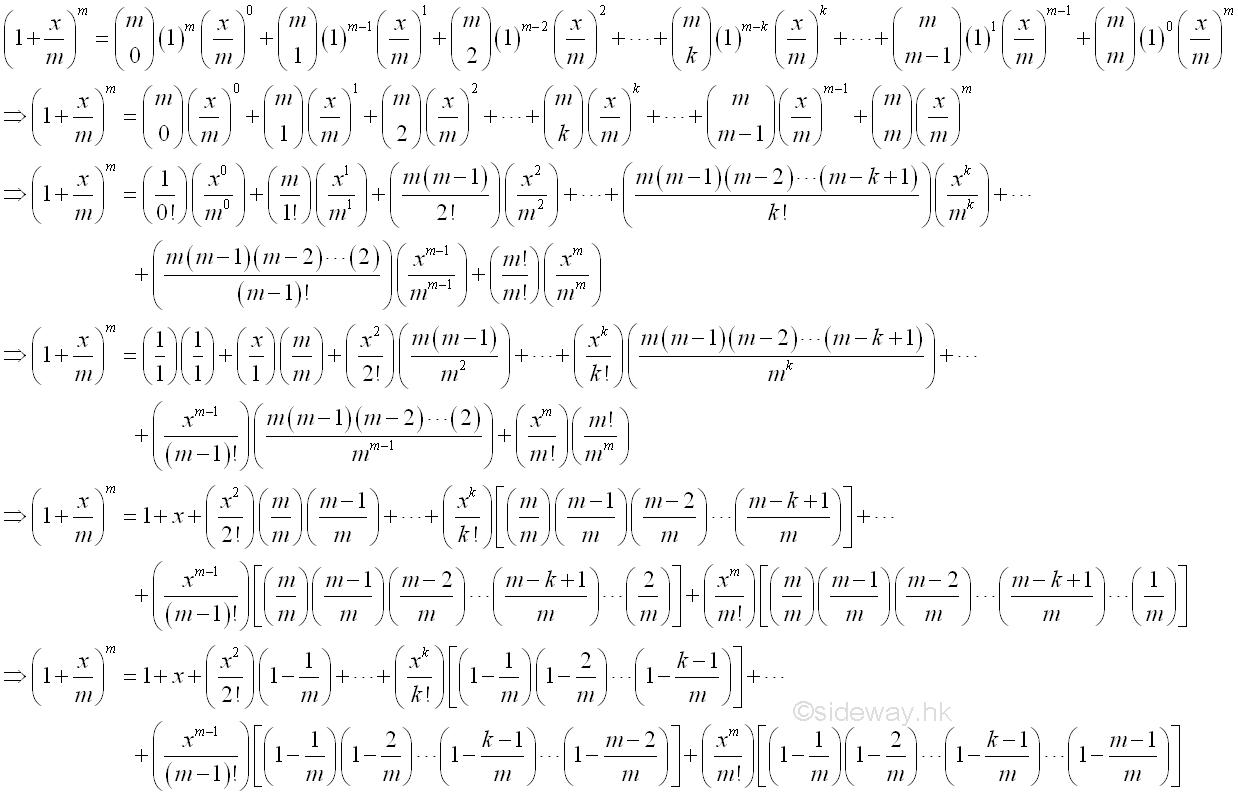
The limit is equal to :
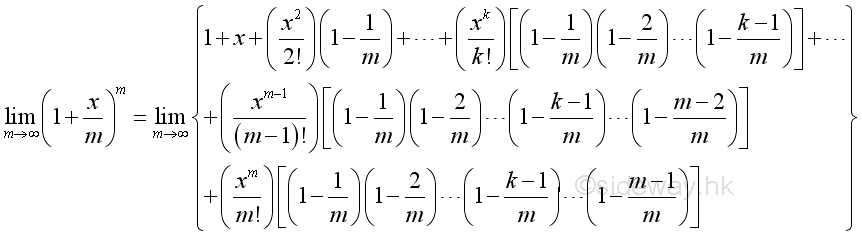
Similar to define the Euler number, the natural exponential function is equal to :
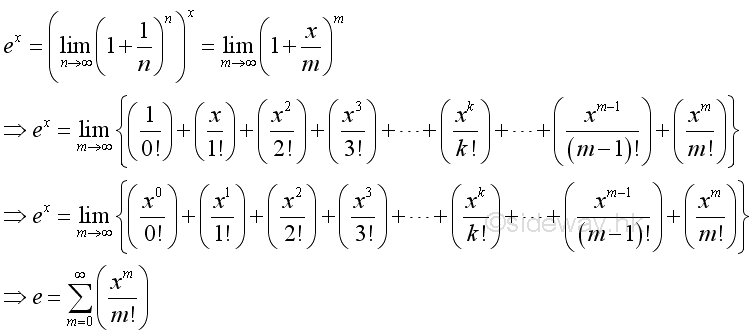
Derivatives of Exponential and Logarithmic Functions
Derivative of Natural Exponential Function

Proof:

Or:
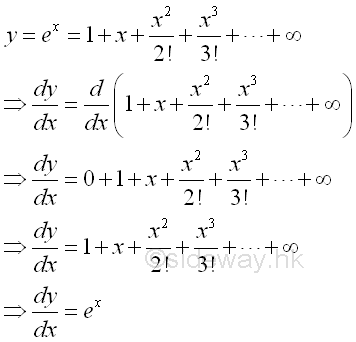
Derivative of Exponential Function
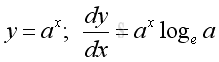
Proof:

Derivative of Natural Logarithmic Function
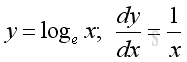
Proof:

Proof for the power function when n is a real number:
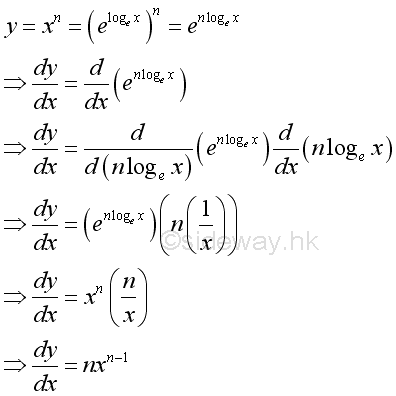
Derivative of Logarithmic Function
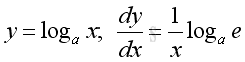
Proof:
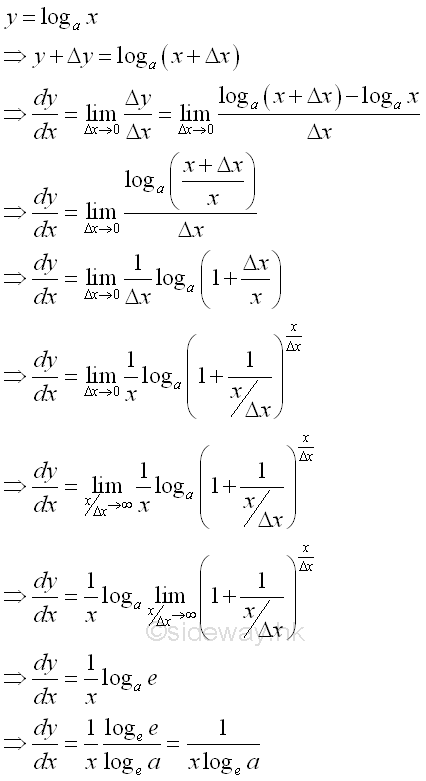
Or:
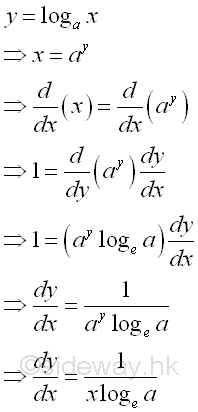
©sideway
ID: 110900007 Last Updated: 7/7/2013 Revision: 2 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
