Content
Interpretations of Derviative
Intantaneous
Rate of Change
Slope of Tagent line
Related Tendency to Change
Linear Approximation Ratio
Curvature Approximation
Interpretations of Derviative
The varieties of interpretations on derviative arise from different approach of applying the deriviative. For a differentiable function y, the definition of derivative of function y is:
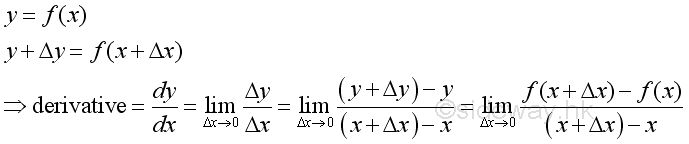
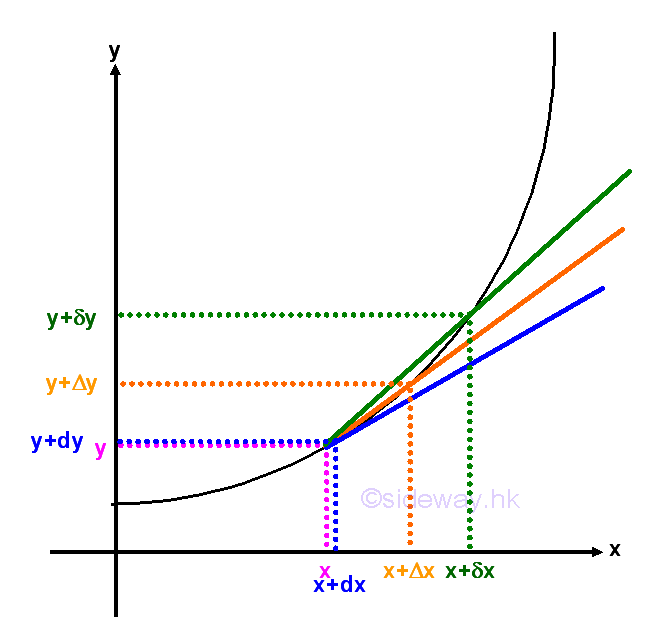
Graphically, the definiation of derivative is
In deriving the derviatives, the limits should exist and then the infinitesimal values of corresponding terms related to Δx are neglected when Δx approaching zero .
Geometrically, since derivative is derived at x, the derivative is the average change of function y between x and Δx. And when Δx approaching zero, the average change of function y becomes very close to actual rate of change at x. Therefore the derivative of function y is also refered to as the instantenous rate of change of function y at x.
And trigronometrically, the slope of a line between two points is the ratio of its vertical distance over its horizontal distance. When Δx approaching zero, the graph of function y between x and Δx can be approximated by a straight line. Therefore the derivative of function y is also refered to as the slope of the function y at x.
Physically, when Δx approaching zero, the derivative of function y with respect to x can be interpreted as the ratio of the tendency to change in infinitesimal dy in response to the change in infinitesimal dx at x.
Therefore the ratio can be used to approximate the change in δy when the change in δx is small. And for a very small, infinitesimal values of dx, the derivative is directly proportional to the ratio of the infinitesimal values dy over the infinitesimal values dx.
Besides, the instantaneous curvature of a point on the curve can also be determined by the differentiation operations through approximation using Pythagorean theorem.
Intantaneous Rate of Change
For simple linear function, the change of function y is proportional to the change of x , therefore the rate of change is constant.
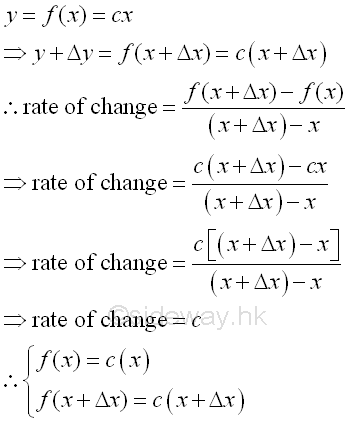
But for nonlinear function, the rate of change is not a constant and varies with x and Δx.
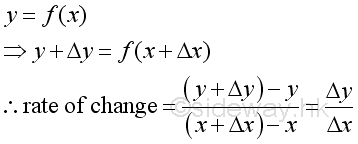
The rate of change can be considered as the average change of function y between x and Δx and is equal to the average rate of change between x and Δx. When reducing the measuring range by decreasing Δx, the average rate of change will become closing to the actural rate of change at x. Therefore when Δx approaching zero, if the limit of the rate of change exist, then the limit is the actual rate of change of the function y at x, or call the instantaneous rate of change of function y at x. The instantaneous rate of change is also a function of x and is called the derivative of function y, that is
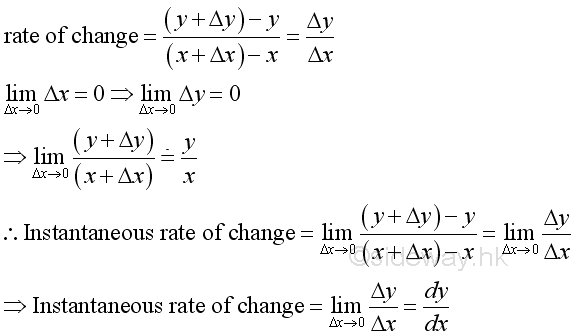
Therefore:
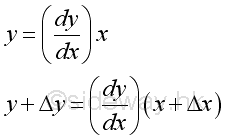
Slope of Tagent line
The value y of a linear function is proportional to x. The solutions of a linear function form a straight line in the xy plane, therefore the constant c of the linear function determines the slope or gradient of that line.
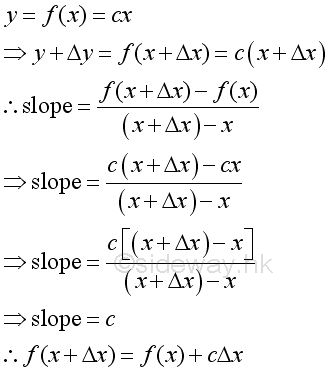
But for nonlinear function, the slope is not a constant and varies with x and Δx.
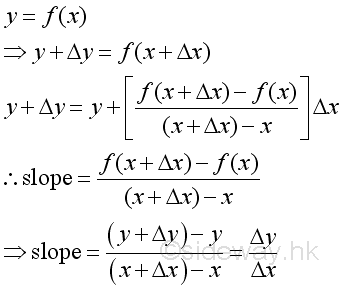
The slope can be considered as the slope of the secant line approximating the graph of function y between x and Δx. And therefore the slope can be used to approimate the slope of the tangent line at x. When decreasing the value of Δx, the secant line will become closing to the actural graph of function y between x and Δx. Therefore when Δx approaching zero, if the limit of the slope exist, then the limit is the actual slope of the tangent line of function y at x, or call the instantaneous slope of function y at x. The instantaneous slope or slope of the tangent line of function y at x is also a function of x and is called the derivative of function y, that is
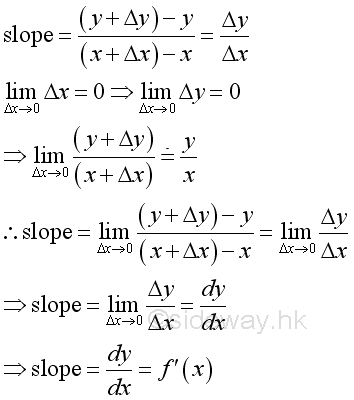
Therefore:
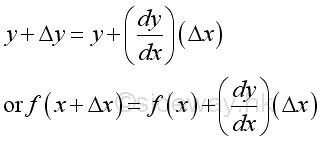
Related Tendency to Change
Derivative can also be interpreted as related tendency to change. Consider the uniform circular motion of an object which rotates around the origin in the xy plane with radius r. The relationship in Cartesian coordinates between x and y is
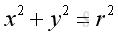
The derivative is
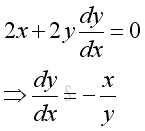
Physically, the ratio of the infinitesimal dy over the infinitesimal dx is equal to the derivative. The ratio can also be interpreted as the tendency to change in infinitesimal dy in response to the infinitesimal dx at x.
Since it is much more convenient to use polar coordinates, with θ representing the angle measured anticlockwise from the x axis, the cartesian coordinates can be transformed to:
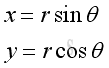
When considering the uniform circular motion of an object as with respect to a common reference θ, the infinitesimals dy and dx are also subject to the same common reference. Therefore, the derivative of function y with respect to x can also be interpreted as the the ratio of the derivative of function y with respect to θ over the derivative of function x with respect to θ. That is the change in infinitesimal dθ will cause the same ratio of changing in infinitesimal dy over infinitesimal dx. The derivative can be expressed as:
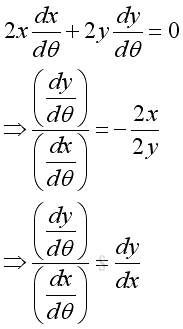
When Δx approaching zero, the derivative can be expressed as the ratio of change in infinitesimal dy in response to the change in infinitesimal dx at x. In other words, the relationship between the infinitesimal dy and the infinitesimal dx at x is fixed by the derivative of function at x also. Therefore the infinitesimal values of dy and dx can also be interpreted as the ratio of tendency to change at x, i.e. dy/dx.
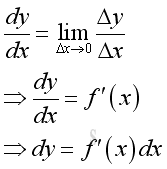
If both y and x can be refered to a common reference and they can also be expressed as a relative function of α, then their derivatives with respect to α remains unchange. This is because the ratio of infinitesimal dy over infinitesimal dx is fixed at x, and the change in the infinitesimal dα can only change the infinitesimals dy and dx in a fixed proportional manner.
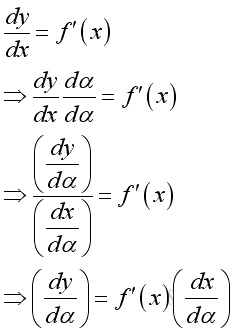
Linear Approximation Ratio
Although derivative is obtained by evatuating when Δx approaching zero, the derivative of function at x can be used as the linear approximation ratio to estimate the function y+δy at x+δx. For example, the linear approximation ratio can be used to estimate the square root of 4.8. The square root function and its derivative are:
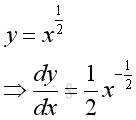
The square root of 4.8 is 2.191 and the approximation is:
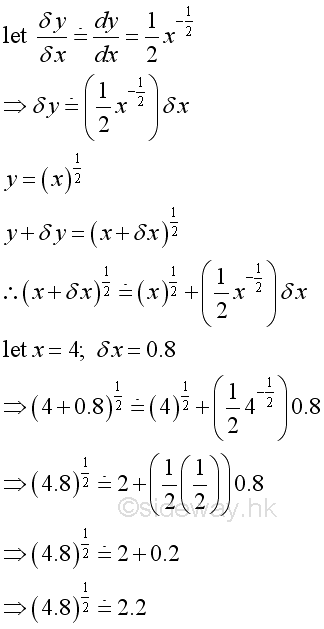
When using derivative of function y=f(x) at x to estimate the solution of a function y+δy=f(x+δ), the ratio of dy/dx is used to estimate the ratio of δy/δx, imply the small change of δy can be approximated by:
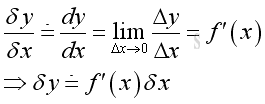
The solution of the function can then be divided into two parts, i.e. the value of y at x plus the value of δy at x+δx. And by making use of the linear approximation ratio f'(x), the solution can be expressed as:
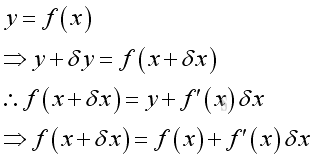
Curvature Approximation
The curvature k at a given point on a curve can be defined as the rate of change of the tangential angle ΔΨ between tangents with respect to the arc length Δs.
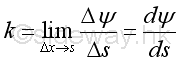
The tangential angle ΔΨ at a point can be determined through the derivative.
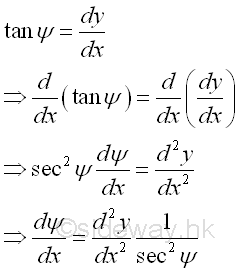
And the arc length Δs can be approximated by the chord length using Pythagorean theorem. Imply
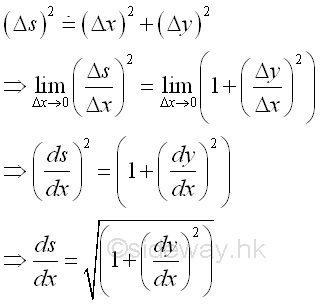
Imply the approximation of curvature is
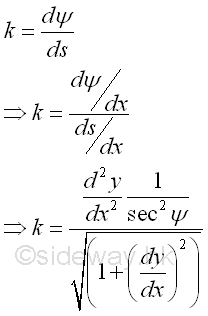
©sideway
ID: 110900011 Last Updated: 11/15/2011 Revision: 3 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
