Content
Rules of Integration for Indefinite
Integral
Subsitution Rule for
Indefinite Integral
Reverse Substitution:
Direct Substitution:
Steps of Integrate by substitution:
Remarks:
Rules of Integration for Indefinite Integral
In order to simplify the task of finding integrals, some integration techniques are developed to help finding integrals by simplifying the integrand to a simple format.
Subsitution Rule for Indefinite Integral
Integration by substitution is method of changing the original variable of an integral to another variable by specifing a relationship between the two variables. The strategy is to simplify the calculation work of determining the value of the integral. The technique is making use of the Rule of Composite Function in differentiation. i.e.
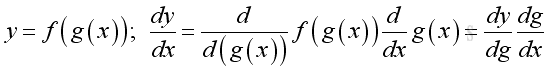
Imply
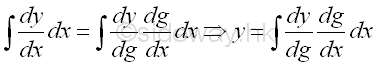
Reverse Substitution:
The method is the application of Rule of Composite Function in differentiation by assuming the method of substitution is already there through the transformation of the orginal integrand to the needed format by re-grouping the original variable as a new variable so as to simplify the calculation work of determining the integral.
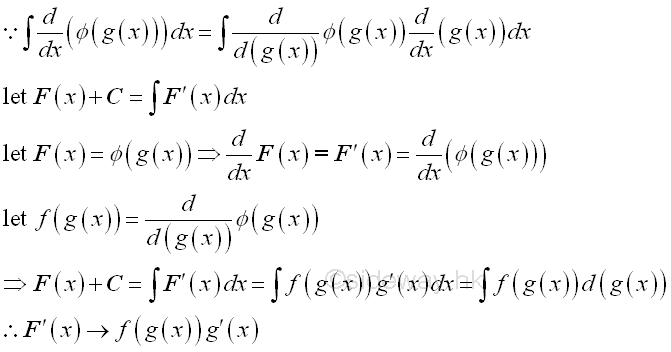
The technique used in the product and quotient of standard function is the application of the substitution function to some standard integral forms by transforming the variable of integration through the decomposition the integrand. Imply:
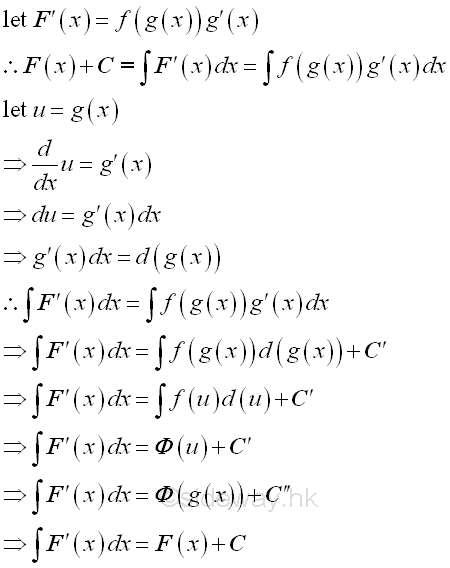
The key step of direct substitution is the formation of another variable u=g(x) from the original variable x of the integrand.
Direct Substitution:
Sometime it is necessary to introduce a new variable of a function for substituting the original variable in order to determine the integrals. The method is the application of Rule of Composite Function in differentiation by applying a direct variable substitution through the transformation of the orginal variable to a new introduced varible by tranforming the original varible of integration to the new variable of integraion indirectly so as to simplify the calculation work of determining the integral. Imply
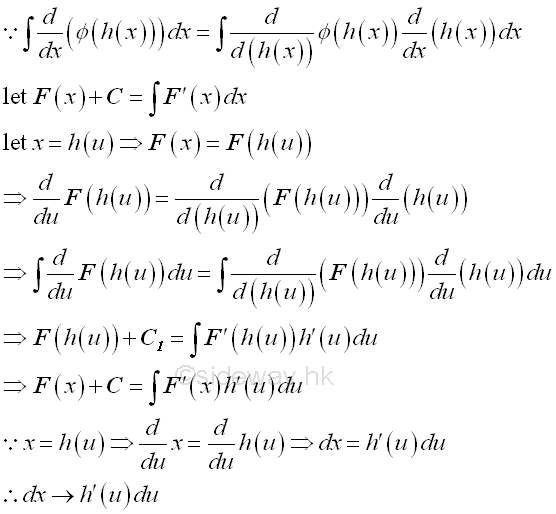
The aim of the technique is to transform the original intergral to another integral that is easier to compute. The strategy of the technique is to transform the integrand and variable of integration into the direction substitution format by introducing a new variable of the function for the original variable so that the transformed integrand of new variable after computing is still easier to determine the integral with respect to the new variable. Imply
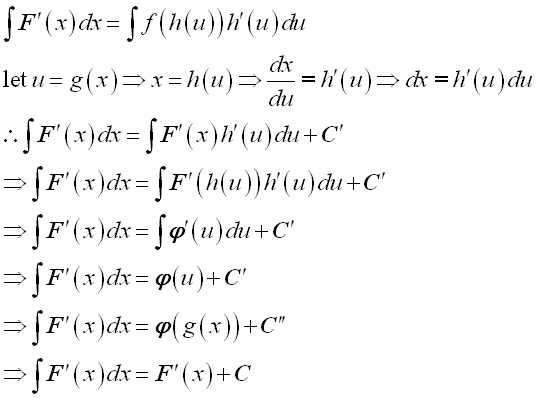
Proof:
Assume the integral of an integrand can be expressed as:
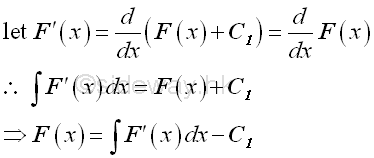
Let x equal to a function h of v be the substitution used, imply:
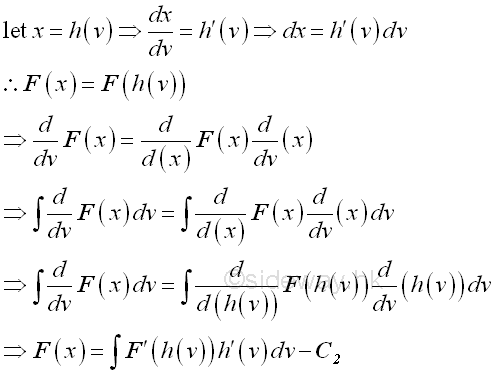
The constant C1 and C2 are constants of integration for two different indefinite integrals. Since F(x)=F(h(v)), imply :
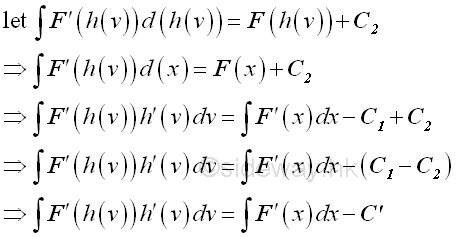
The different between two indefinite integrals is a constant C', therefore the original integral can be determined by applying the forward substitution of the new introduced variable first and then substite the backward substitution back to the solution to obtain the original variable.
The two important steps of the substitution rule are:
-
The substitution of the substitution function of new introduced variable v. The transformation of variable can be applied to the original function directly through direct substitution.:
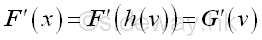
-
The variable of integration dx can be transformed through differentiation with respect to the new introduced variable v.
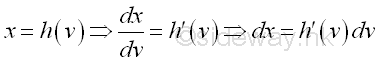
Therefore:
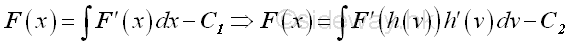
Steps of Integrate by substitution:
-
Start with the original integral
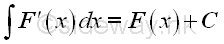
-
Introduce a new variable u for substiting the original variable x.
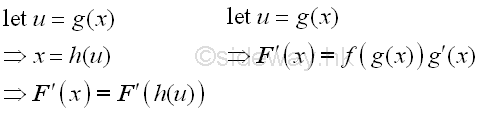
-
Find the relationship between the variables of integration du and dx through differentiation.
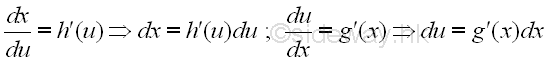
-
Substitute new variable u and new variable of integration du into the original integrand.
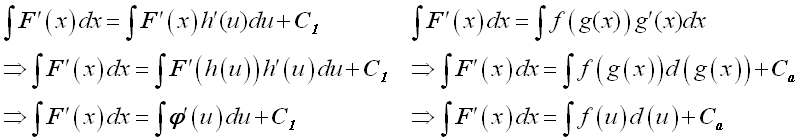
-
Integrate the transformed integrand.
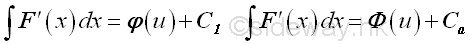
-
Subsitute back the orginal varibale x by taking the inverse of function of u.
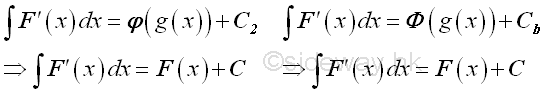
-
Check the solution by differentiation.
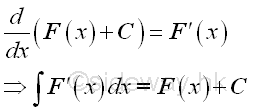
Remarks:
For definite integral, the domain should be considered also, imply
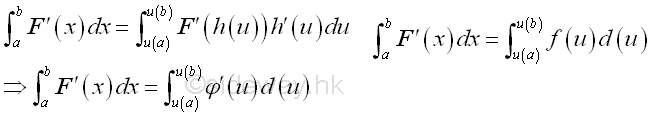
©sideway
ID: 111000024 Last Updated: 10/25/2011 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
