Content
Second Moment of An Area
Rectangular
Moment of Inertia of an Area
Elemental Horizontal Strip
Elemental Vertical Strip
Elemental Rectangular Strip about the referenc axis
perpendicular to the length
Polar
Moment of Inertia of an Area
Elemental Arc Strip
Elemental Sector Slice
Second Moment and First Moment of an Area
Radius of Gyration of an Area
Parallel-Axis Theorem
Second Moment of An Area
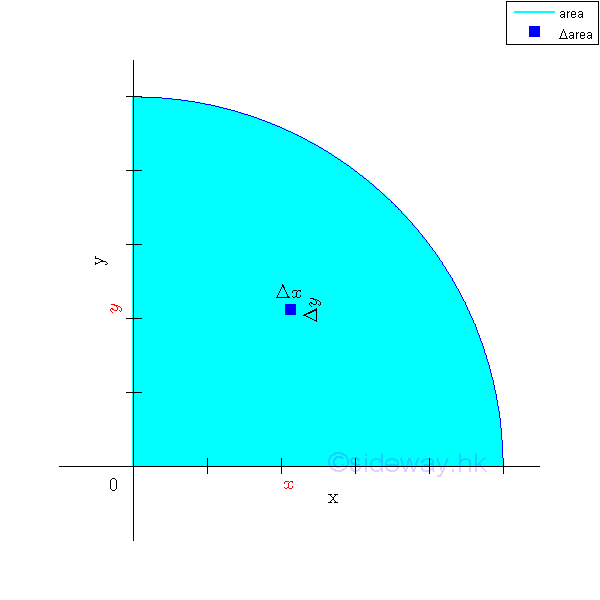
By definition, second moment of an area about an axis is equal to the summation of the products of the square of the distance between the elemental area and the reference axis, and the elemental area over an area.
Rectangular Moment of Inertia of an Area
The two most common second moments are the rectangular moments of inertia of an area about the two coordinate axes. Imply
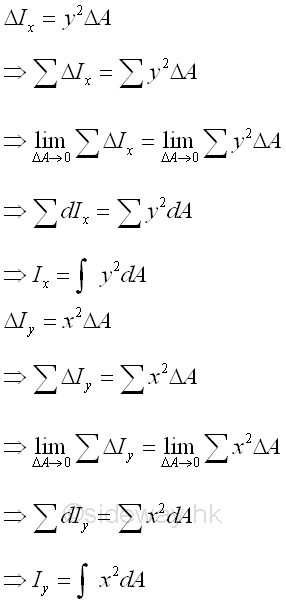
The elemental differential area is defined as a second order element of dxdy. And a double integration is needed to determine the second moment of an area.
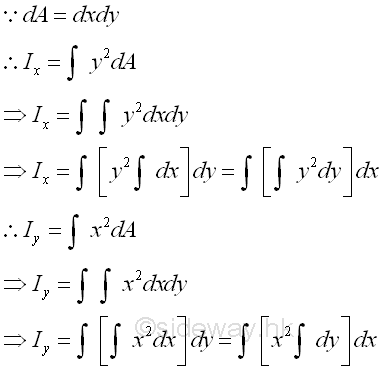
However, when a group of second order elements can be grouped into a first order element, the elemental differental area can then be expressed as a first order element e.g. a rectangular strip. Only a single integration is needed to determine the second moment of an area.
Elemental Horizontal Strip
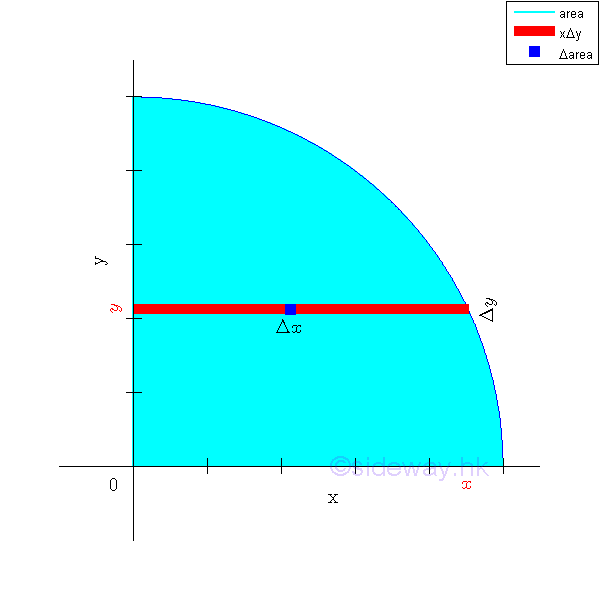
When the second order element areas can be grouped as a first order element, e.g. a horizontal rectangular strip by neglecting the higher order term, only a single integration is needed to determine the second moment of an area. Since the elemental area of a horizontal strip have the same distance from the x-axis. Imply
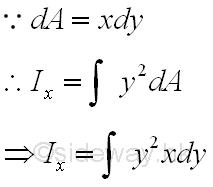
Elemental Vertical Strip
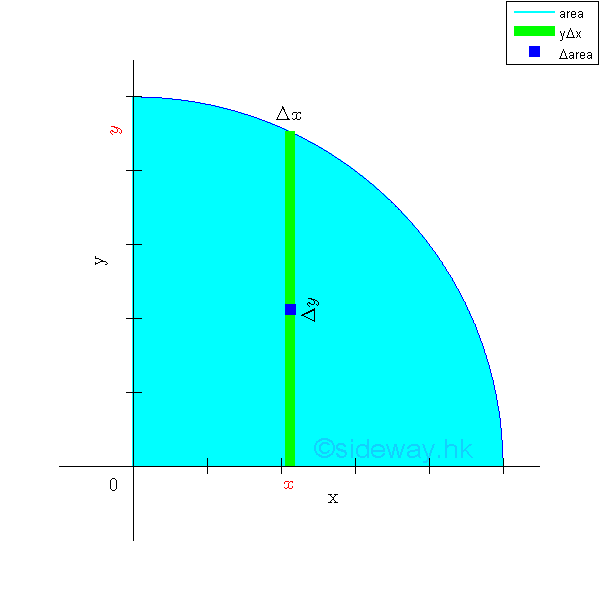
When the second order element areas can be grouped as a first order element, e.g. a vertical rectangular strip by neglecting the higher order term, only a single integration is needed to determine the second moment of an area. Since the elemental area of a vertical strip have the same distance from the y-axis. Imply
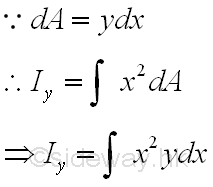
Elemental Rectangular Strip about the referenc axis perpendicular to the length
Because of the distance between the reference axis and elemental area of the rectangular strip is not a constant when the reference axis is not parallel to the lenght of the elemental rectangular strip, the second order differential area element cannot be replaced by the first order differential area element directly. However, the second order differential area element can be replaced by the first order differential area element, if the distance can be expressed as the function along the reference axis or the length of the elemental rectangular strip. For a horizontal elemental rectangular strip, the second moment about an vertical axis is
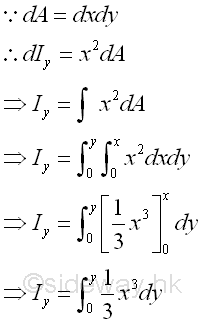
For a vertical elemental rectangular strip, the second moment about an horizontal axis is
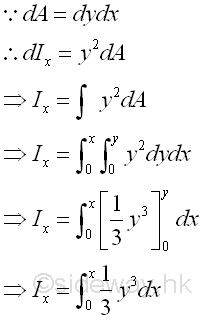
Polar Moment of Inertia of an Area
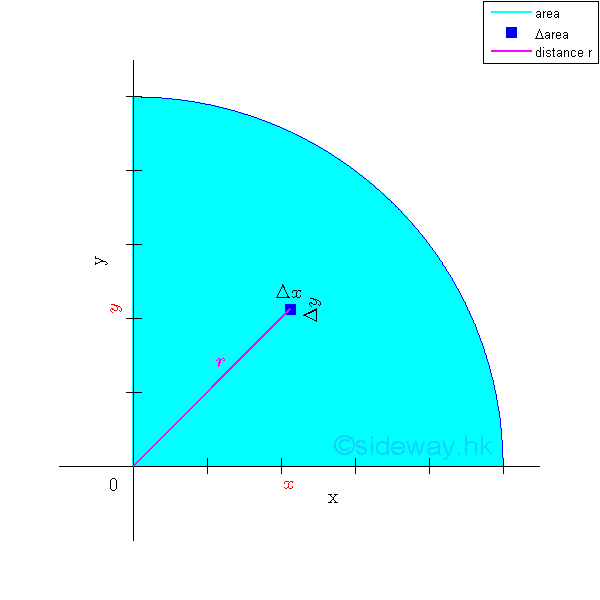
Besides the rectangular moments of inertia, another important second moment of an area is the polar moment of inertia, which is the second moment of an area about the axis normal to the planar area. And usually the polar moment of inertia of the area is defined with respect to the z axis or the pole at the origin O. Imply
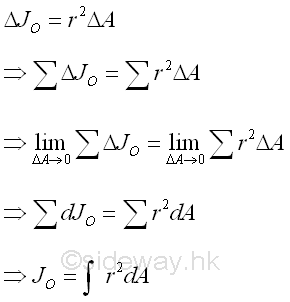
By considering the same second order differential area element, the polar moment of inertia of the area can be determined from the rectangular moments of inertia, Ix and Iy if the two rectangular moments of inertia are known using the perpendicular axis theorem. Imply
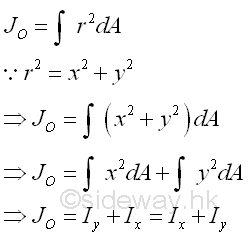
If the bounding profile of the area is expressed in form of polar coordinates, the polar moment of inertia about the pole can also be determined by the second moment of an area with the second order differential polar area element. Imply
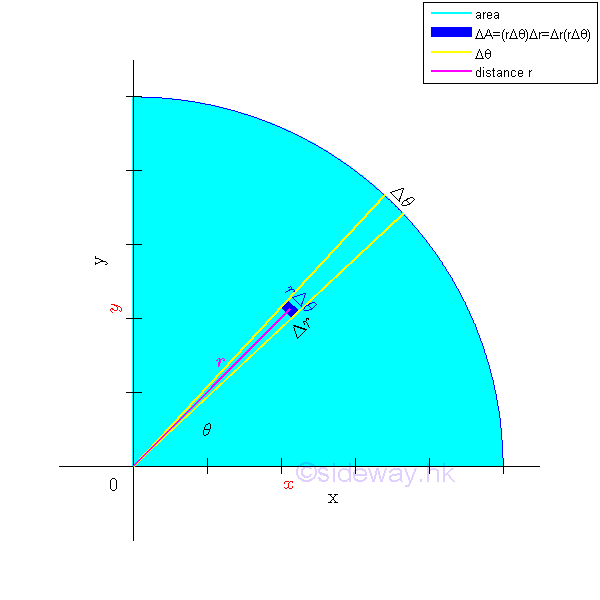
Imply
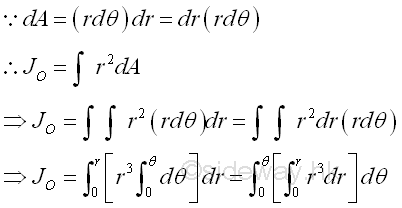
Or the polar moment of inertia about the pole can be determined by the second moment of an area with the first order differential polar area element.
Elemental Arc Strip
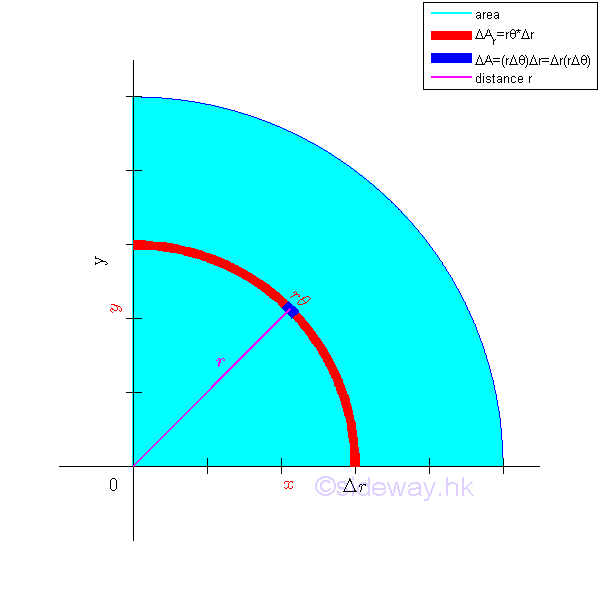
The polar moment of inertia about the pole can be determined by the second moment of an area with the first order differential elemental arc strip. Since the distance between the differential elemental area and the pole is the same. Imply
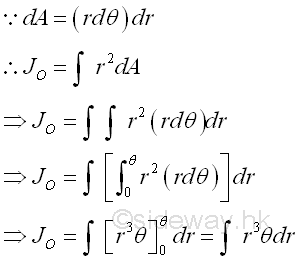
Elemental Sector Slice
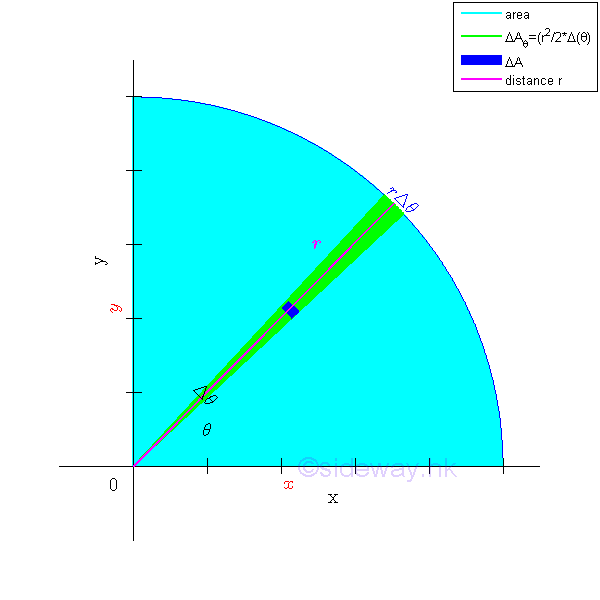
The polar moment of inertia about the pole can be determined by the second moment of an area with the first order differential elemental sector slice. Since the distance between the reference axis and elemental area of the sector slice is not a constant, the second order differential area element cannot be replaced by the first order differential area element directly. However, the second order differential area element can be replaced by the first order differential area element, if the distance can be expressed as the function along the reference pole or the radius of the elemental sector slice. For an elemental sector slice, the second moment about the pole is
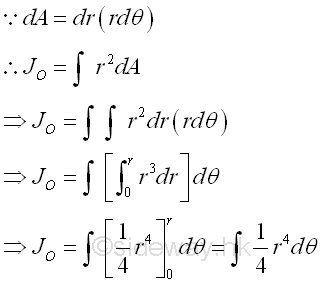
Second Moment and First Moment of an Area
The value of first moment can be positive, negative and zero. But the second moment is always positive because the area element is alway positive, and the square of the distance is also alway positive. And therefore both the rectangular moment of inertia and the polar moment of inertia must be positive regardless of the location of the area element locating on the coordinate system.
Besides, the dimension of second moment of an area is of length to the fourth power, while the first moment of an area had dimensions of length to the third power.
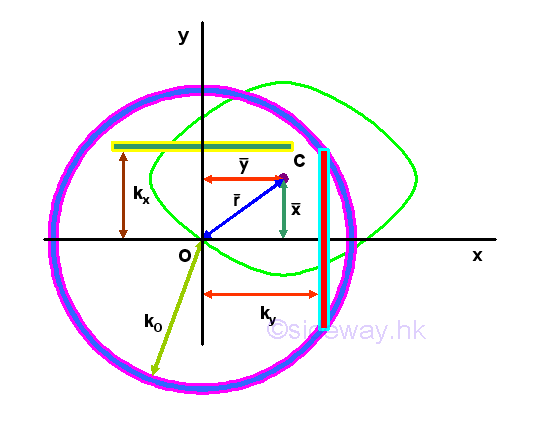
Radius of Gyration of an Area

For an area, the first moment of the area about an axis or a point can be expressed as product of the imaginary total area of the area at the centroid of the area and the shortest distance between the centroid of the area and the reference axis or the reference point. But for the second moment of the area, there is only an distance, called the radius of gyration, i.e. kx or ky, to describe the distance between the location of an imaginary total area strip of the area and the reference axis or pole such that an equivalent second moment of the area is created by assuming the imaginary total area of the area is placed at this distance away from the reference axis. Or similarly the polar radius of gyration, kO about the pole. Imply
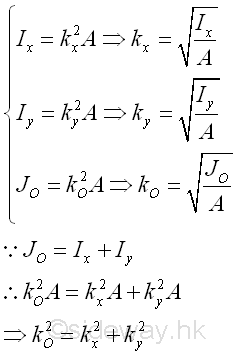
Imply
Parallel-Axis Theorem
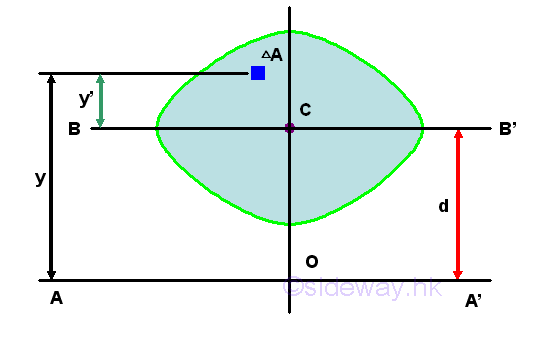
Unlike the first moment about the axis passing through the centroid, i,.e. the centroidal axis, the second moment about the axis, BB' passing through the centroid is not equal to zero. And the second moment of an area, A about the axis passing through its centroid is called the centroidal moment of inertia I of the area. Imply
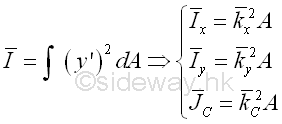
Consider the moment of inertia I of the area A about the axis, AA'. Imply
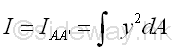
The distance y in the integral can be expressed in terms of the distances y' and d. Imply
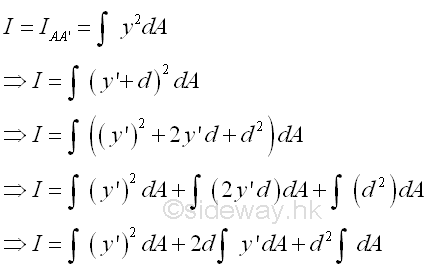
The integral of the moment of inertia I of the area A about the axis, AA' can be divided into three seperated integrals. The first integral is the centroidal moment of inertia I of the area. The second integral is the first moment of the area A about the centroidal axis and the value of the first moment of the area about the centroidal axis is equal to zero. The third integral is equal to the total area only. The square of the distance d is alway positive also, therefore the third term is alway positive regardless of the location of the parallel reference axis. Imply
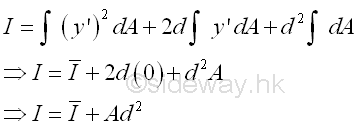
Therefore the second moment of an area A about an axis AA' is equal to the second moment of an area A about the centroidal axis BB' parallel to the reference axis AA' plus the product of the area A and the square of the distance d between the two parallel axes. This is called the parallel-axis theorem. Similarly, the theorem can also be applied to the polar moment of inertia about a pole O. Imply
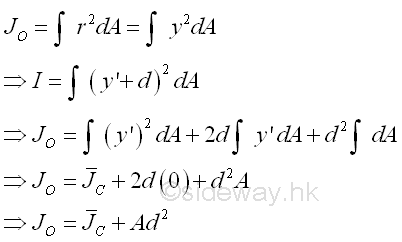
The theorem can also be expressed in terms of the radius of gyration of an area. Imply
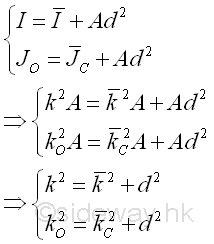
Since the theorem can only be used to relate the second moment of an area about an axis with the second moment of an area about the centroidal axis parallel to the reference axis, two second moments of an area about two parallel axes can not be transferred directly. e.g.
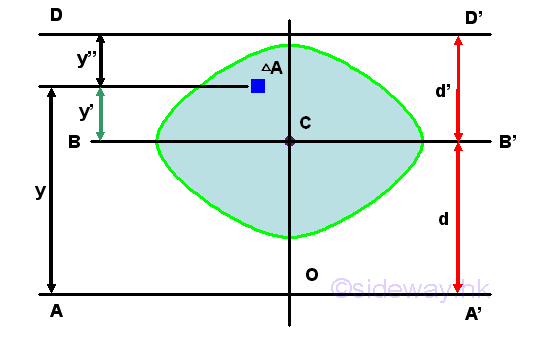
Imply
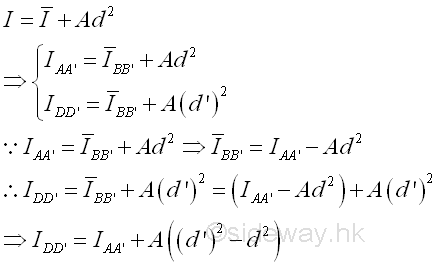
©sideway
ID: 121000002 Last Updated: 10/16/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)
- Tefal BL83SD PerfectMix Cook Blender(last updated On 11/25/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/24/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/23/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/22/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
