Content
Second Moment of An Area of Geometric Shape
Moment of Inertia of Areas
Second Moment of Area of Semi-circle
Second Moment about x by
Double Integration
Second Moment about y' by Double Integration
Polar Moment about O from Rectangular Moments of Inertia
Second Moment of Area of
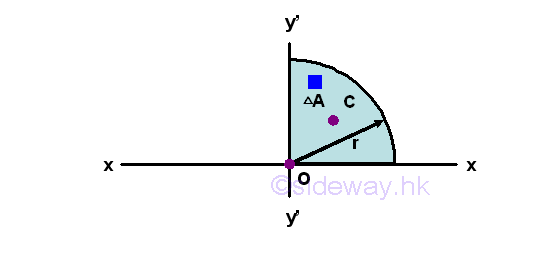
Quarter-circle
Second Moment about x by
Double Integration
Second Moment about y' by Double Integration
Polar Moment about O from Rectangular Moments of Inertia
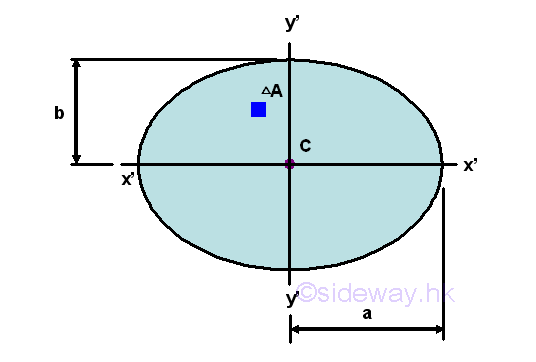
Second Moment of Area of Ellipse
Second Moment about x'
by Double Integration
Second Moment about y' by Double Integration
Polar Moment about C from Rectangular Moments of Inertia
Second Moment of An Area of Geometric Shape
The second moment of an area of a geometric shape can be determined by integration or the parallel-axis theorem. Imply
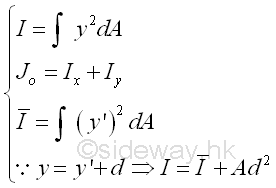
Moment of Inertia of Areas
Second Moment of Area of Semi-circle
Second Moment about x by Double Integration
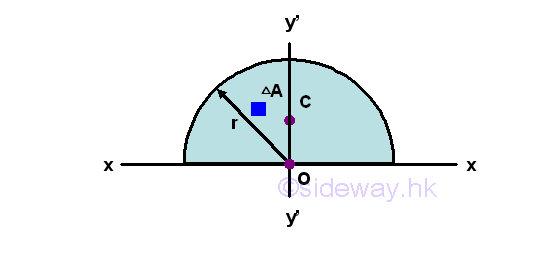
The second moment of an area of a semicircle about the axis x is
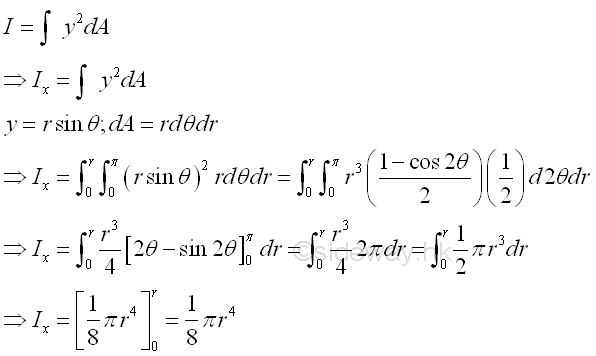
Second Moment about y' by Double Integration
The second moment of an area of a rectangle about the centroidal axis y' is
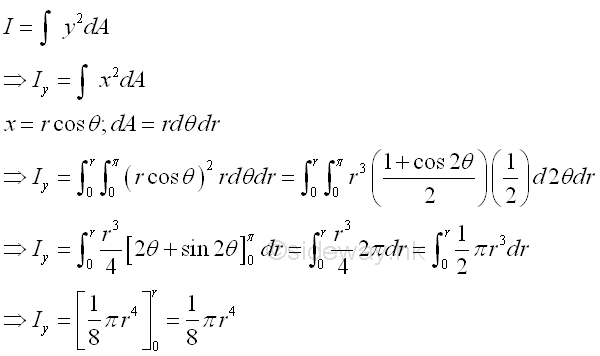
Polar Moment about O from Rectangular Moments of Inertia
The polar moment of an area of a rectangle about the center O is
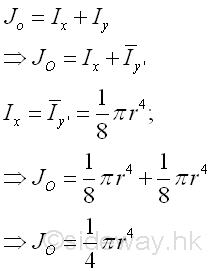
Second Moment of Area of Quarter-circle
Second Moment about x by Double Integration
The second moment of an area of a semicircle about the axis x is
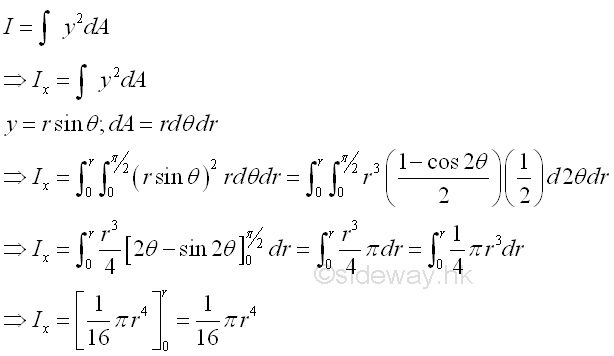
Second Moment about y' by Double Integration
The second moment of an area of a rectangle about the centroidal axis y' is
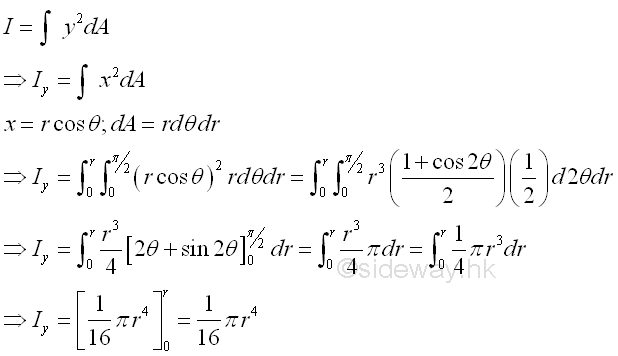
Polar Moment about O from Rectangular Moments of Inertia
The polar moment of an area of a rectangle about the center O is
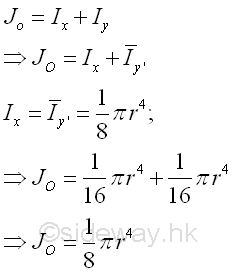
Second Moment of Area of Ellipse
Second Moment about x' by Double Integration
The second moment of an area of a ellipse about the centroidal axis x' is
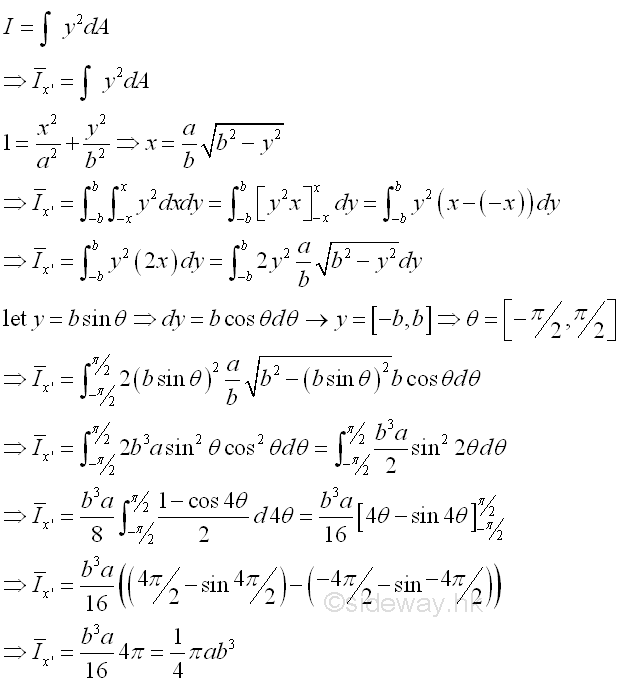
Second Moment about y' by Double Integration
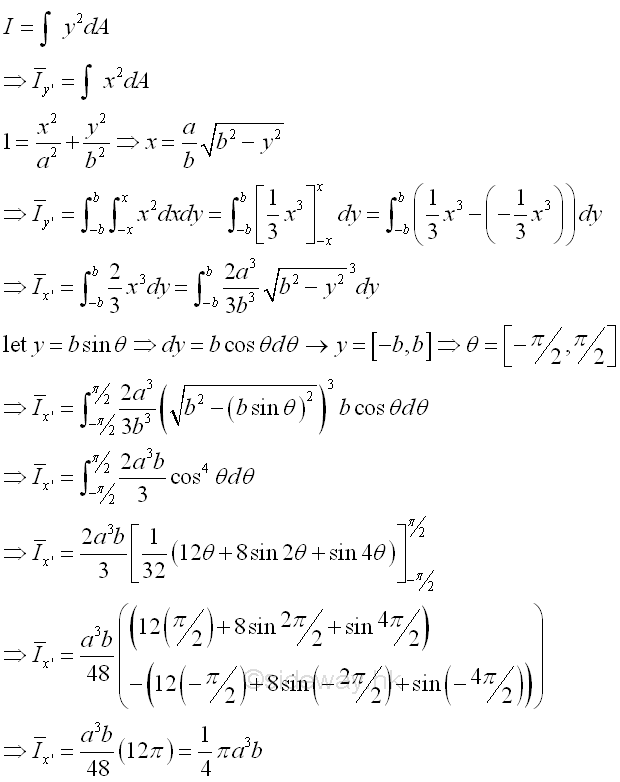
Polar Moment about C from Rectangular Moments of Inertia
The polar moment of an area of a circle about the centroid C is
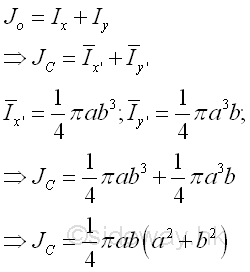
©sideway
ID: 121000008 Last Updated: 10/18/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Mandai(last updated On 12/8/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/7/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 24
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
