Content
First Moment of
Three Dimensional Body
Centroidal Plane
Symmetry
of 3D Body
First Moment of Three Dimensional Body
The first moment of a three dimensional body is defined as the summation of the moments of all elements of the shape of the three dimensional body about a plane. The first moment of a three dimensional body is the mathematical measure of the distribution of the shape of a three dimensional body about a plane. The first moment of a three dimensional body can be used to detemine the centroid of the an object. The first moment of a three dimensional body is usually called the first moment of volume with respect to a plane.
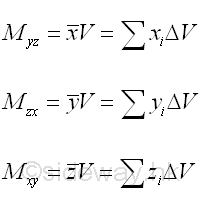
In practical problems, the centroid of an three dimensional object is determined by the first moment of a three dimensional body with the method of the first moment of volume.
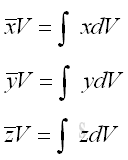
Centroidal Plane
Although the value of first moment of a volume is dependent on the reference planes due to the change of reference, the location of the centroid of a volume is independent of the reference planes and is the property of the volume only.

If the first moment of an volume about an axis is equal to zero, the centroid of the area must be located on the plane. Conversely, if the centroid of an volume is located on an plane, the first moment of the volume must be equal to zero also. e.g. the plane xy, yz, and zx have their origin at the centroid.
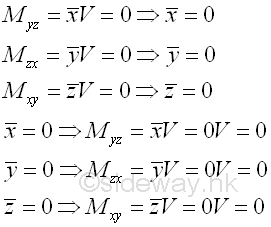
The planes pass through the centroid of a volume are called centroidal planes. The first moments of volume about any centroidal plane of the volume are zero. Since the centroid is located on the centroidal plane, the perpendicular distance from the centroid to the centroidal plane must be zero also.
Symmetry of 3D Body
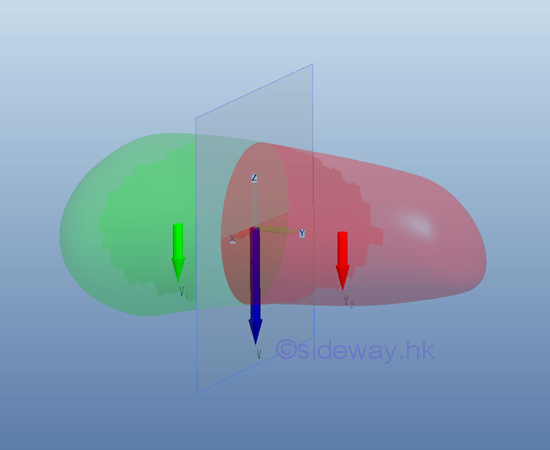
A centroidal plane always divide the three dimensional body into two distinct subregions. Since the first moment of volume of a three dimensional body about its centroidal plane is equal to zero, the two first moment of volume of the two distinct subregions about the centroidal plane of the three dimensional body should be equal and opposite in sense. Imply
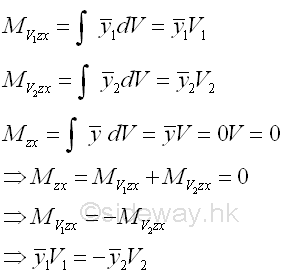
Considering the two subregions of a symmetrical three dimensional body on either side of the plane of symmetry, the elemental areas are equal in size and are equidistant from the plane. For every elemental area on one side of the plane of symmetry, there alway exists an elemental area on the opposite side of the plane of symmetry. And the first moment of these elemental areas will cancel each other because the distances are equal and opposite in sense. Therefore the first moment of a symmetrical three dimensional body about the plane of symmetry is equal to zero and the centroid of the symmetrical three dimensional body should always lies in the symmetric plane also. e.g. by the extrusion of symmetrical body section
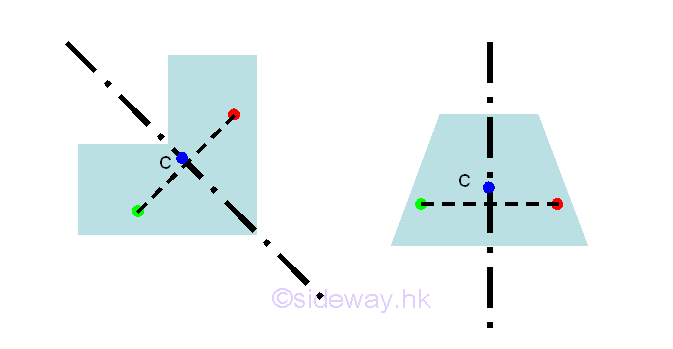
Since the centroid of a symmetrical three dimensional body always lies in the symmetric plane, when a plane body possesses two or more planes of symmetry, the centroid of the plane body should always be located in the intersection of the symmetric planes. e.g. by the extrusion of symmetrical body section
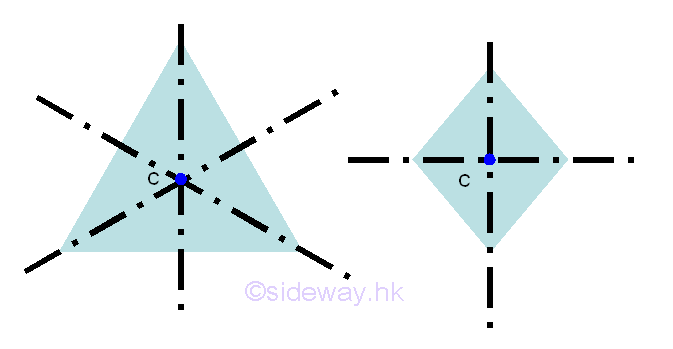
Similarly, the centroid of three dimensional bodies with two or more planes of symmetry should always be located in the intersection of the symmetric planes by constructing the planes of symmetry of the three dimensional body. e.g. by the extrusion of symmetrical body section
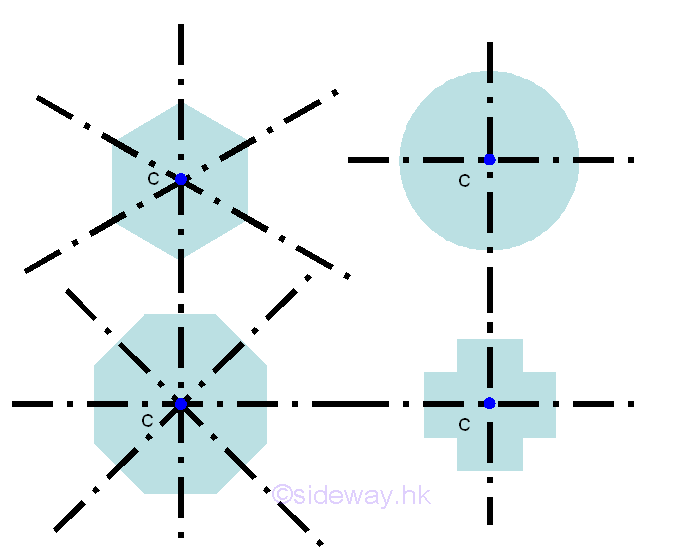
Besides the reflection symmetry, a symmetrical three dimensional body can also be rotational symmetric about a point. Geometrically, for every element at coordinate x,y, there always exist an element at coordinate -x,-y. Therefore, a symmetrical three dimensional body with two planes of symmetry at right angle to each other is always symmetric about an axis of intersection. From the above symmetry three dimensional bodies, the centroids of the three dimensional bodys always lies on the axis of intersection, i.e. intersection of two symmetry planes. However, a rotational symmetric three dimensional body sometime does not necessary to be symmetric about an axis. e.g. by the extrusion of symmetrical body section
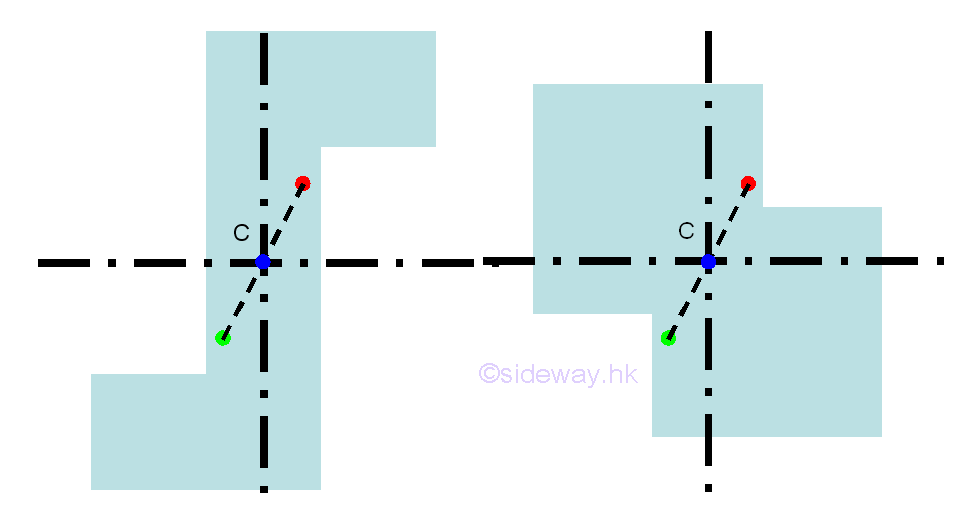
The three dimensional body formed by the extrusion of symmetrical body section can be constant or variable. For example, a square body section: right prism or regular pyramid. a circle body section: right cylinder or regular cone.
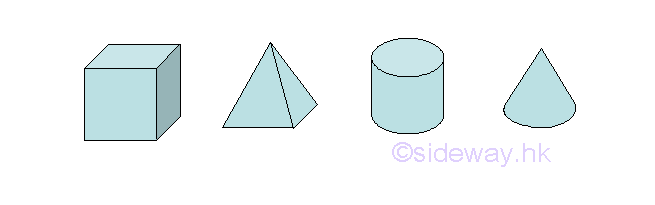
However, for a symmetrical three dimensional body with three planes of symmetry at right angle to each other is always symmetric about the point of intersection. From the above symmetry three dimensional bodies, the centroids of the three dimensional bodys always lies on the point of intersection, e.g. cube, sphere
Another important type of symmetrical three dimensional body is the solid of revolution. e.g. sphere, cone. The symmetrical plane always pass through the axis of revolution and therefore the centroid of a symmetrical three dimensional body is located on the axis of revolution.
©sideway
ID: 120600010 Last Updated: 6/15/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Schneider Electric(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)
- Tefal BL83SD PerfectMix Cook Blender(last updated On 11/25/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/24/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/23/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/22/2025)
- Panasonic EH-5282 Hair Dryer(last updated On 11/21/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 53
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
