Content
Centroid
of Volume by Geometric Decomposition
Centroids of Composite 3D Body
Centroid of composite
3D body 1
Centroid of composite 3D body 2
Centroid of Volume by Geometric Decomposition
By denoting the position of the element of a 3D body relative to the coordinate system as xi,yi,zk, the coordinates x, y, z , of the center of gravity of the plane body where the resultant force W applied can be determined by equating the moment of the resultant force W about the yz plane, zx plane and xy plane and the corresponding mements of elements of the 3D body about the coordinate axis respectively. Imply.
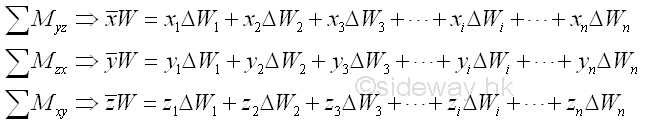
Therefore the coordinates x , y , and z of the center of gravity of the plane body is.
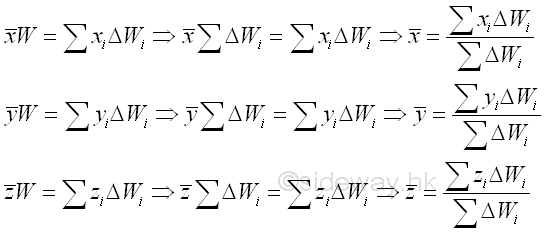
If a 3D body can be divided into some common 3D bodys, the 3D body can be considered as a composite 3D body. For a composite 3D body, the cooresponding mements of elements of the plane body can also be grouped according to the composition of the 3D body. Imply
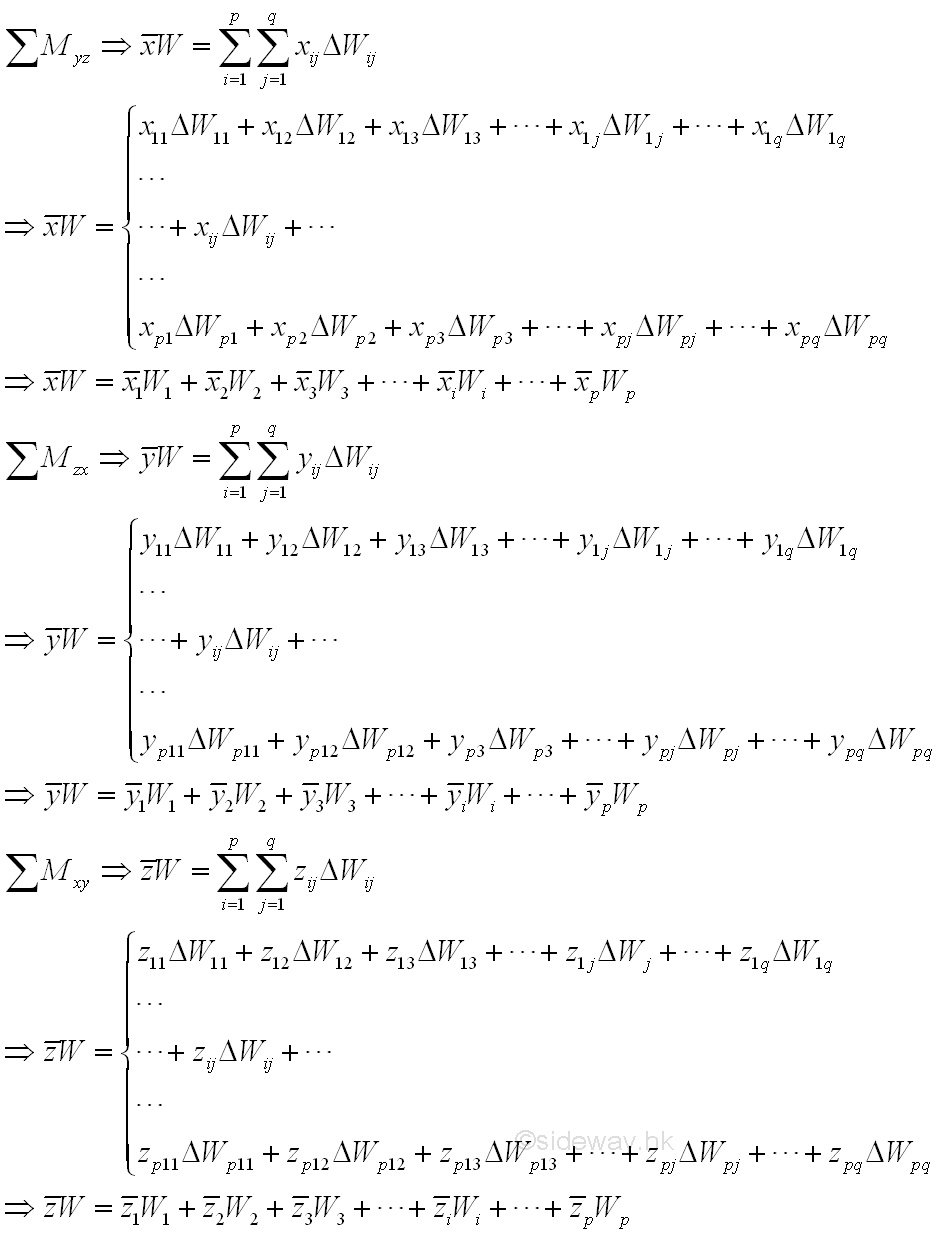
For a homogeneous 3D body, the first moment of the 3D body volume is
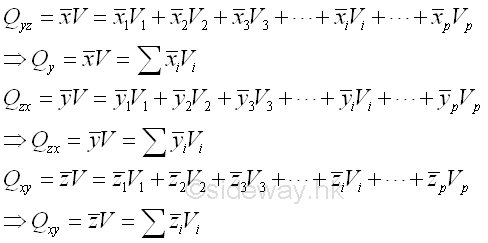
Centroids of Composite 3D Body
Centroid of composite 3D body 1
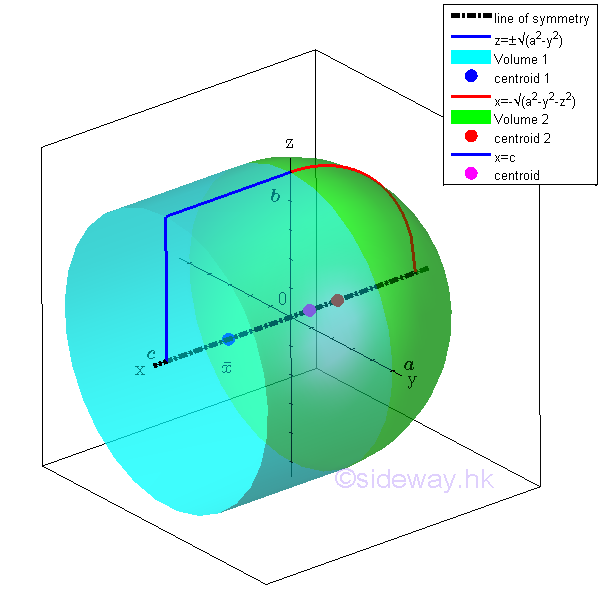
For example, the signed volume of a composite 3D body bounded by surfaces in rectangular form , Imply
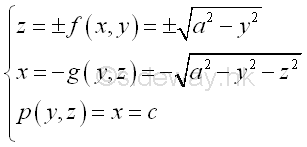
The composite 3D volume can be divided into two common shapes. Therefore, centroid of the bounded volume by concept of composite 3D body is
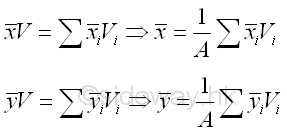
The volume of the 3D body is
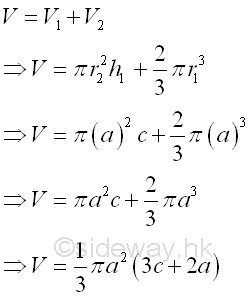
Coordinate x of centroid
The first moment of area can be either positive and negative. The centroid of volume 1 is located to the positive side of the yz plane, the first moment of volume is positive. Since the centroid of volume 2 is located to the negative side of the yz plane, the first moment of area is negative and the negative sign is usually assigned to the x coordinate of the centroid of volume 2. Imply
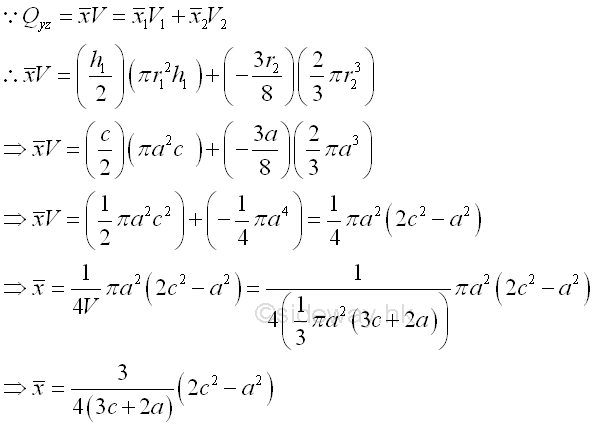
Similarly if the coordinate x of centroid of 3D volume is positive, the coordinate x of the centroid is located to the positive side of yz plane.
Coordinate y and z of centroid
By symmetry, the coordinate y and z of centroid lie on the x axis, the line of symmetry.
Centroid of composite 3D body 2
Since the first moment of volume of a hole can be considered as the negative sense of the first moment of volume by assuming the first moment of volume of the same volume of negative sense. Therefore the first moment of volume of a hole is negative. The negative sign is usually assigned to the volume of the hole and the volume of a hole is called negative volume.
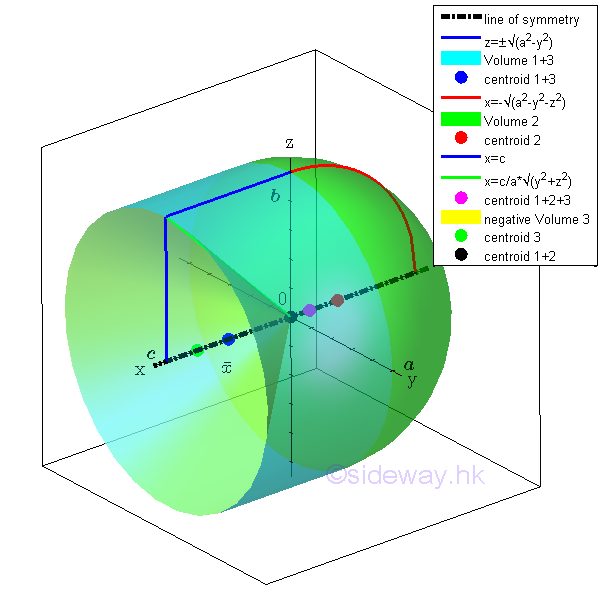
For example, the signed volume of a composite 3D volume bounded by surfaces in rectangular form , Imply
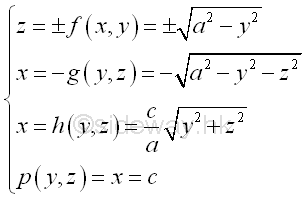
The 3D volume body can be divided into common shapes. Therefore, centroid of the bounded voulme by concept of composite 3D volume body is
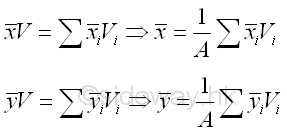
The volume of 3D body is
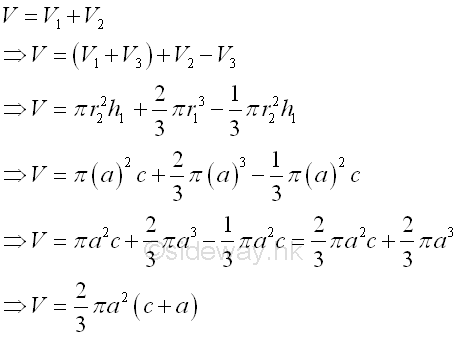
Coordinate x of centroid
The first moment of volume can be either positive and negative. The centroid of volume 1 plus volume 3 is located to the positive side of the yz planes, the first moment of volume is positive. Since the centroid of volume 2 is located to the negative of the yz planes, the first moment of volume is negative and the negative sign is usually assigned to the x coordinate of the centroid of volume 1. And for the centroid of hole, negative volume 3 is located to the positive side of the yz planes, the coordinate of the centroid of volume 3 is positive but the sense of the volume is negative. Imply
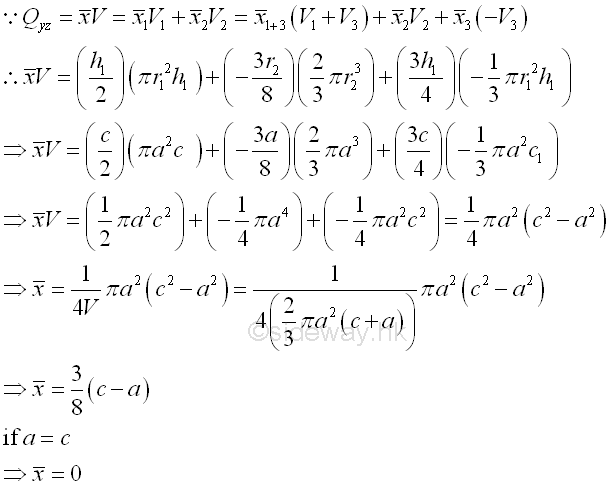
If c is equal to a, the coordinate x of centroid of volume of the 3D body is located on the origin 0 of x axis.
Coordinate y and z of centroid
By symmetry, the coordinate y and z of centroid lie on the x axis, the line of symmetry.
©sideway
ID: 120700004 Last Updated: 7/12/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Space(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 35
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
