Content
Charge Density
Electric Field of Charged Rod
Electric Field in the Bisecting Plane
Procedure for Calculating Electric Field of Distributed Charges
Source and Reference
Charge Density
For a simple 1d charged rod of length L in meter has total charge 𝑄. Assuming there are 10 point charges in a row then
Electric Field of Charged Rod
The electric field of charged rod can be calcuted as following∆𝑥=𝐿/10⇒∆𝑞=𝑄/10=(𝑄/𝐿)∆𝑥
𝐿=∑
∆𝑥=∫
𝑑𝑥
𝑄=∑
∆𝑞=𝑄𝐿
∑
∆𝑥=𝑄𝐿
∫
𝑑𝑥
Electric Field in the Bisecting Plane
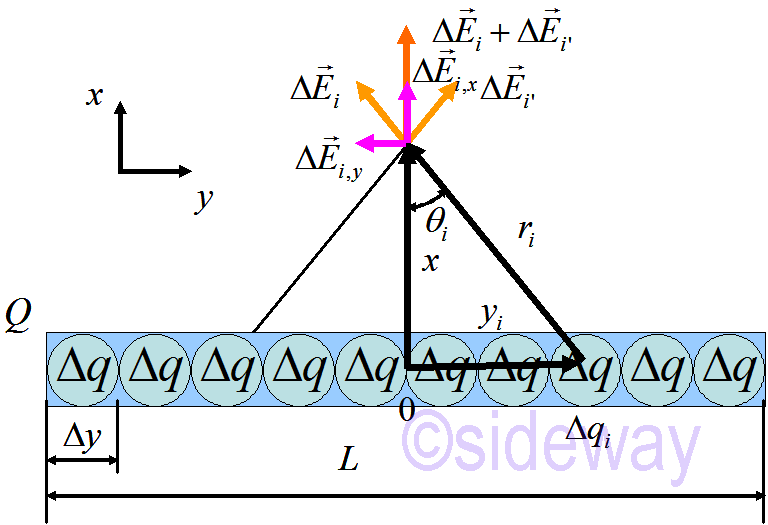 The electric field in the bisecting plance can be determined as following
The electric field in the bisecting plance can be determined as following
𝑟=(𝑥2+𝑦2)1/2 and sin 𝜃=𝑥𝑟𝑖
𝐸
𝑡𝑜𝑡=∑𝑖
∆𝐸
𝑖=∑𝑖
∆𝐸𝑖,𝑥𝑥
∆𝐸𝑖,𝑥=|∆𝐸
𝑖|cos(𝜃)
=14𝜋𝜀0
∆𝑞𝑟2𝑖
𝑥𝑟𝑖
=∆𝑞4𝜋𝜀0
𝑥(𝑥2+𝑦2𝑖)3/2
𝐸
𝑡𝑜𝑡=∑𝑖
∆𝑞4𝜋𝜀0
𝑥(𝑥2+𝑦2𝑖)3/2
𝑥
=14𝜋𝜀0
𝑄𝑥𝐿
𝐿/2∫−𝐿/2
𝑑𝑦(𝑥2+𝑦2𝑖)3/2𝑥
=14𝜋𝜀0
𝑄𝑥𝑥2+(𝐿/2)2𝑥
For an infinite rod
𝐿→∞; 𝑄→∞ ⇒𝑄𝐿
→𝜆
Where 𝜆 is defined as charge per unit length.
𝐸
𝑡𝑜𝑡=14𝜋𝜀0
𝑄𝑥𝐿
∞∫−∞
𝑑𝑦(𝑥2+𝑦2𝑖)3/2𝑥
=14𝜋𝜀0
𝑄𝑥𝐿
2𝑥2𝑥
=14𝜋𝜀0
2𝜆𝑥
𝑥
𝐸
𝑡𝑜𝑡=14𝜋𝜀0
𝑄𝑥𝑥2+(𝐿/2)2𝑥
𝐸
𝑡𝑜𝑡=14𝜋𝜀0
2𝜆𝑥
𝑥
Procedure for Calculating Electric Field of Distributed Charges
- Cut the charge distribution into pieces for which the field is known.
- Write an expression for the electric field due to one piece
- Choose origin
- Write an expression for ∆𝐸 and its components
- Add up the contributions of all the pieces
- Try to integrate symbolically
- If impossible-integrate numerically
- Check the results
- direction
- Units
- special cases
Source and Reference
https://www.youtube.com/watch?v=pJwg2Bk0BDE&list=PLZ6kagz8q0bvxaUKCe2RRvU_h7wtNNxxi&index=5
©sideway
ID: 191101802 Last Updated: 11/18/2019 Revision: 0
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
