Content
Electric Potential
Potential Difference
Non-uniform Electric Field
Path of Potential Difference
Source and Reference
Electric Potential
For two fixed opposite charged plates, the electric field due to plates is as following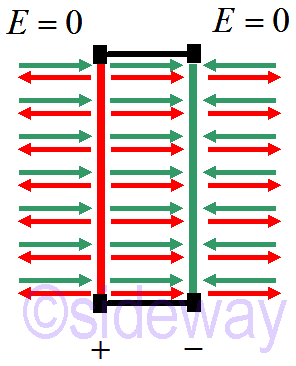 If a charged particle is placed in the capacitor, an induced force will drive the charged particle to move.
If a charged particle is placed in the capacitor, an induced force will drive the charged particle to move.
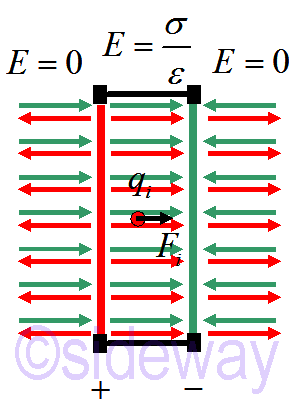 The eletric pontential energy acting on the charge particle 𝑞𝑖 is
The eletric pontential energy acting on the charge particle 𝑞𝑖 is
𝑈ele= ∑𝑗
𝑈𝑖𝑗= ∑𝑗
14𝜋𝜀0
𝑞𝑖𝑞𝑗𝑟𝑖𝑗
The electric potential is defined as the potential or the ability to have potential energy if a test charge enters the system.
In other words, the electric potential can be expressed as
𝑉≡𝑈ele𝑞
=JoulesCoulomb
=[Volts]
Potential Difference
When the charge particle is moved from 𝑎 to 𝑏 as following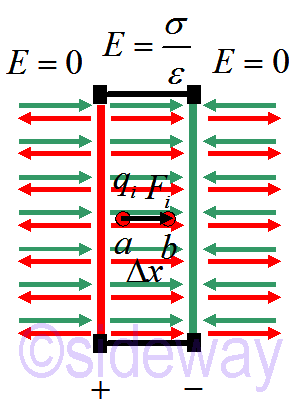 the change in potential energy of the system is
the change in potential energy of the system is
∆𝑈=−𝑊internal=−∫
𝑞𝐸
∙𝑑𝑟
=−𝑞∫
𝐸𝑥𝑑𝑥
⇒∆𝑈=−𝑞𝐸∆𝑥
In which the systems tends to lower their potential energy by moving the charge particle from a higher potential energy position to a lower potential energy position. In other words, the potential difference drive the charge particle to move from one position to another.
∆𝑈=−𝑞𝐸∆𝑥≡𝑞∆𝑉⇒∆𝑉=∆𝑈𝑞
=−𝐸∆𝑥
𝑉=[Volt]=JouleCoulomb
∆𝑈/𝑞=−𝐸∆𝑥≡∆𝑉⇒𝐸=−∆𝑈/𝑞∆𝑥=−∆𝑉/∆𝑥
|𝐸|=JouleCoulomb-meter
=NewtonCoulomb
=VoltMeter
An electron-Volt, 𝑒𝑉 is the energy required to move a charge particle, 𝑞=1𝑒=1.6×10−19𝐶 through 1𝑉. That is 1.6×10−19𝐽=1𝑒𝑉
Non-uniform Electric Field
For a uniform electric field, i.e. 𝐸∥𝑥, ∆𝑉=−𝐸∆𝑥. And for a uniform electric field pointing in any direction.∆𝑉=−(𝐸𝑥∆𝑥+𝐸𝑦∆𝑦+𝐸𝑧∆𝑧)≡−𝐸
∙𝑑𝑟
If the electric field 𝐸 is not uniform, but varies in space. The potential difference can be determined by a line integral like stepping along a path. At each step, use component of electric field parallel to the step direction.
∆𝑉=−𝑓∑𝑖
𝐸
∙𝑑𝑙
=−𝑓∫𝑖
𝐸
∙𝑑𝑙
The electric field can therefore be expressed as
𝐸
=−𝑑𝑉𝑑𝑥
=−∂∂𝑥𝑉
𝑥
+∂∂𝑦𝑉
𝑦
+∂∂𝑧𝑉
𝑧
∇
𝑉Path of Potential Difference
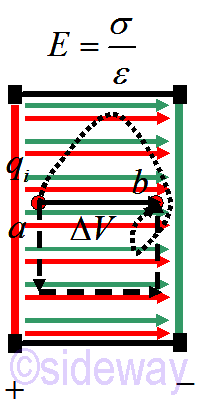 Since electricity is a conservative force the potential difference ∆𝑉 is independent of the path taken. For example, in a simple uniform electric field
Since electricity is a conservative force the potential difference ∆𝑉 is independent of the path taken. For example, in a simple uniform electric field
∆𝑉=−𝑓∑𝑖
𝐸
∙𝑑𝑙
=−𝑓∑𝑖
𝐸𝑥𝑑𝑙𝑥+𝑓∑𝑖
𝐸𝑦𝑑𝑙𝑦+𝑓∑𝑖
𝐸𝑧𝑑𝑙𝑧
Source and Reference
https://www.youtube.com/watch?v=8HSwBeHZoao&list=PLZ6kagz8q0bvxaUKCe2RRvU_h7wtNNxxi&index=9
©sideway
ID: 191200302 Last Updated: 12/3/2019 Revision: 0
Latest Updated Links
- Philips CL400 Ceiling Light 13W(last updated On 10/30/2025)
- Ikea TISKEN basket(last updated On 10/29/2025)
- Ikea TISKEN towel rack(last updated On 10/28/2025)
- Ikea REXBEGONIA mattress protector(last updated On 10/27/2025)
- Ikea KEJSAROLVON mattress protector(last updated On 10/26/2025)
- Ikea KVARNVEN ergonomic pillow(last updated On 10/25/2025)
- Ikea BRUKSVARA pocket prung mattress(last updated On 10/24/2025)
- Ikea VÅGSTRANDA pocket sprung mattress super firm(last updated On 10/23/2025)
- Ikea VITVAL underbed(last updated On 10/22/2025)
- Ikea SLÄKT bed frame with slatted bed base(last updated On 10/21/2025)
- ASUS TUF ESD-T1A External SSD Enclosure(last updated On 10/20/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 23![]()
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
