Current Density and Conductivity

The current density 𝐽 is the current per unit area 𝐴, 𝐼=|𝑞|𝑛𝐴𝑣=|𝑞|𝑛𝐴𝑢𝐸
𝐽≡𝐼𝐴=|𝑞|𝑛𝐴𝑢𝐸𝐴=|𝑞|𝑛𝑢𝐸 The conductivity 𝜎 is a mterial-dependent quantity. 𝐽=|𝑞|𝑛𝑢𝐸≡𝜎𝐸⇒𝜎=|𝑞|𝑛𝑢 Conductivity add, even for opposite sign charge carriers That is 𝜎=|𝑞+|𝑛+𝑢++|𝑞−|𝑛−𝑢−

Resistance

The resistance of a resistor of length 𝐿, ∆𝑉=−∫𝐸⋅𝑑𝑙⇒|∆𝑉|=𝐸𝐿
𝐼=𝑞𝑛𝐴𝑢𝐸=𝜎𝐴𝐸
𝐼=𝜎𝐴𝐸=𝜎𝐴|∆𝑉|𝐿⇒|∆𝑉|=𝐼𝐿𝜎𝐴
∵|∆𝑉|=𝐼𝑅⇒𝑅=𝐿𝜎𝐴

Resistors in Series

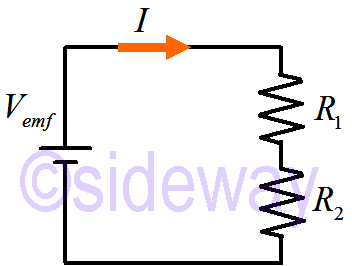When resistors are in series, the effective series resistance is 𝐼=𝐼1=𝐼2
∆𝑉emf+∆𝑉1+∆𝑉2=0
⇒𝑉emf−𝐼𝑅1−𝐼𝑅2=0
⇒𝑉emf=𝐼𝑅1+𝐼𝑅2=𝐼(𝑅1+𝑅2)=𝐼𝑅equivalent
⇒𝑅equivalent=𝑅1+𝑅2 For resistor made of the same material and with the same 𝐴, the resistance follows straight from the definition of resistance 𝑅=𝐿𝜎𝐴 𝑅equivalent=𝐿1𝜎𝐴+𝐿2𝜎𝐴=𝐿1+𝐿2𝜎𝐴=𝐿equivalent𝜎𝐴
⇒𝐿equivalent=𝐿1+𝐿2

Resistors in Parallel

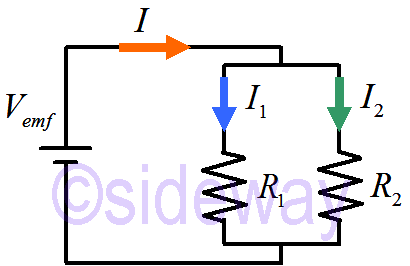When resistors are in parallel, the effective parallel resistance is 𝐼=𝐼1+𝐼2=𝑉emf𝑅1+𝑉emf𝑅2=1𝑅1+1𝑅2𝑉emf=1𝑅equivalent𝑉emf
⇒1𝑅equivalent=1𝑅1+1𝑅2=𝑅1+𝑅1𝑅1𝑅1 For resistor made of the same material and with the same 𝐿, the resistance follows straight from the definition of resistance 𝑅=𝐿𝜎𝐴 𝑅=𝐿𝜎𝐴⇒1𝑅=𝜎𝐴𝐿
⇒1𝑅equivalent=𝜎𝐴1𝐿+𝜎𝐴1𝐿=𝜎𝐿(𝐴1+𝐴2)=𝜎𝐿𝐴equivalent
⇒𝐴equivalent=𝐴1+𝐴2

Capacitor in Series

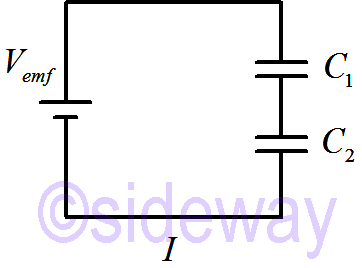When capacitors are in series, the effective series capacitance is 𝐼=𝐼1=𝐼2⇒𝑄1=𝑄2=𝑄
∆𝑉emf+∆𝑉1+∆𝑉2=0
⇒𝑉emf−𝑄𝐶1−𝑄𝐶2=0
⇒𝑉emf=𝑄𝐶1+𝑄𝐶2=𝑄1𝐶1+1𝐶2=𝑄1𝐶equivalent
⇒1𝐶equivalent=1𝐶1+1𝐶2=𝐶1+𝐶2𝐶1𝐶2 For capacitor made of the same material and with the same 𝐴, the capacitance follows straight from the definition of capacitance 𝐶=𝜀₀𝐴𝑠 𝐶=𝜀0𝐴𝑠⇒1𝐶=𝑠𝜀0𝐴
⇒1𝐶equivalent=𝑠1𝜀0𝐴+𝑠2𝜀0𝐴=1𝜀0𝐴(𝑠1+𝑠2)=1𝜀0𝐴𝑠equivalent
⇒𝑠equivalent=𝑠1+𝑠2

Capacitor in Parallel

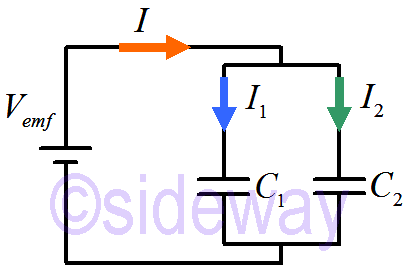When capacitors are in parallel, the effective parallel capacitance is 𝐼=𝐼1+𝐼2⇒𝑄=𝑄1+𝑄2
⇒𝐶equivalent𝑉emf=𝐶1𝑉emf+𝐶2𝑉emf
⇒𝐶equivalent=𝐶1+𝐶2 For capacitor made of the same material and with the same 𝑠, the capacitance follows straight from the definition of capacitance 𝐶=𝜀₀𝐴𝑠 𝐶equivalent=𝜀0𝐴1𝑠+𝜀0𝐴2𝑠=𝜀0𝑠(𝐴1+𝐴2)=𝜀0𝑠𝐴equivalent
⇒𝐴equivalent=𝐴1+𝐴2

Source and Reference

https://www.youtube.com/watch?v=C0hFkY2G4y4&list=PLZ6kagz8q0bvxaUKCe2RRvU_h7wtNNxxi&index=18