Content

Time Constant of RC Circuit
 Current in RC Circuit
 Source and Reference

Time Constant of RC Circuit

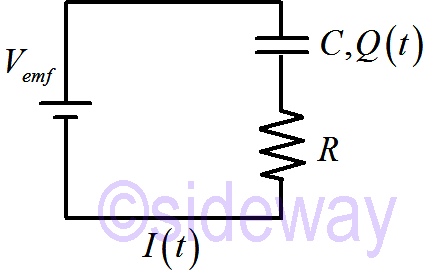Immediately after the RC circuit is connected to battery, 𝑄=0; 𝑉_𝑒𝑚𝑓=𝐼𝑅 After the capacitor is fully charged, 𝑄=𝐶𝑉_𝑒𝑚𝑓; 𝐼=0

Current in RC Circuit

The current in RC Circuit is a function of time. Current is defined as Charge ∆𝑄 passed by per unit time ∆𝑡

𝐼=|𝑞|𝑛𝐴𝑣⇒𝐼=∆𝑄∆𝑡

        lim ∆𝑡→0⇒𝐼=𝑑𝑄𝑑𝑡

Since current 𝐼 is the same everywhere in the RC circuit, charge ∆𝑄 passed by per unit time ∆𝑡 throughout the circuit piles up at the capacitor 𝐶. The voltage 𝑉_𝐶 across the capacitor is 𝑄𝐶 and voltage 𝑉_𝑅 across the resistor is 𝐼𝑅. Apply voltage loop

𝑉_𝑒𝑚𝑓=𝑉_𝐶+𝑉_𝑅=𝑄𝐶+𝐼𝑅=𝑄𝐶+𝑑𝑄𝑑𝑡𝑅

⇒𝑑𝑄(𝑡)𝑑𝑡=𝑉_𝑒𝑚𝑓𝑅−1𝑅𝐶𝑄(𝑡)

Assume 𝑄(𝑡) has the form 𝐴𝑒^{−𝑡/𝑅𝐶}+constant,

𝑄(𝑡)=𝐴𝑒^{−𝑡/𝑅𝐶}+constant⇒𝑑𝑄(𝑡)𝑑𝑡=−1𝑅𝐶𝐴𝑒^{−𝑡/𝑅𝐶}=−1𝑅𝐶𝑄(𝑡)−constant
         =1𝑅𝐶constant−1𝑅𝐶𝑄(𝑡)=𝑉_𝑒𝑚𝑓𝑅−1𝑅𝐶𝑄(𝑡)
        ⇒constant=𝑉_𝑒𝑚𝑓𝐶⇒𝑄(𝑡)=𝐴𝑒^{−𝑡/𝑅𝐶}+𝑉_𝑒𝑚𝑓𝐶

Apply boundary conditions, At 𝑡=0, 𝑄=0

𝑄(𝑡→0)=𝐴𝑒^{−0/𝑅𝐶}+𝑉_𝑒𝑚𝑓𝐶=𝐴+𝑉_𝑒𝑚𝑓𝐶=0⇒𝐴=−𝑉_𝑒𝑚𝑓𝐶

Therefore

𝑄(𝑡)=(−𝑉_𝑒𝑚𝑓𝐶)𝑒^{−𝑡/𝑅𝐶}+𝑉_𝑒𝑚𝑓𝐶=𝑉_𝑒𝑚𝑓𝐶1−𝑒^{−𝑡/𝑅𝐶}

 I(𝑡)=𝑑𝑄𝑑𝑡=−𝑉_𝑒𝑚𝑓𝐶−1𝑅𝐶𝑒^{−𝑡/𝑅𝐶}=𝑉_𝑒𝑚𝑓𝑅𝑒^{−𝑡/𝑅𝐶}

𝑅𝐶 is the time constant of a RC circuit. When time 𝑡=𝑅𝐶, the current 𝐼 drops by a factor of 𝑒.

I(𝑡)=𝑉_𝑒𝑚𝑓𝑅𝑒^{−𝑡/𝑅𝐶}=𝑉_𝑒𝑚𝑓𝑅𝑒⁻¹=12.718𝑉_𝑒𝑚𝑓𝑅=0.37𝑉_𝑒𝑚𝑓𝑅

By Talor Expansion 𝑒^{−𝑡/𝑅𝐶}=1−𝑡𝑅𝐶+𝑡𝑅𝐶^²12−⋯ When time 𝑡 and 𝑅𝐶 are equal, the coefficients of Taylor Expansion equal to 1. In other words, at the time constant 𝑅𝐶 the current is always reduced to 0.37 of the original current.