ElectricElectric ForcePolarizationInsulatorElectric Field of Charged RodElectric Field of Charged Ring, Disk, and PlaneElectric Field of Charged Spherical ShellPotential EnergyPotential DifferenceElectric PotentialElectric EnergyElectric CurrentMagnetic FieldKirchhoff's Current LawSteady StateCapacitor Charge and DischargeRC Circuit Time ConstantCurrent Density, ConductivityMagnetic ForceElectricity, MagnetismMotor, GeneratorGauss's LawAmpere's LawFaraday's Law, Lenz's LawSuperconductor, InductorMaxwell's EquationsWave Equation
Draft for Information Only
Content
Electric flux
Gauss's Law
Gauss's Law for Point Charge
Gauss's Law for Plane
Gauss's Law for Magnetism
Source and Reference
Electric flux
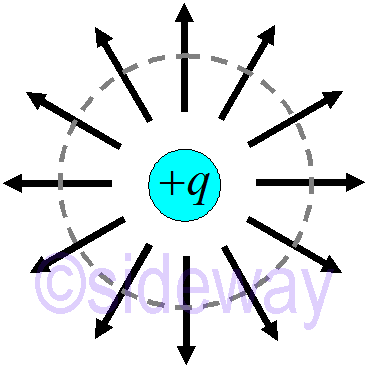 The source of electric field is charge. When there is electric field flowing radially, there is a source inside. Electric flux is defined as the effect of electric field over the area of the surface projected in a plane perpendicular to the field, that is (
The source of electric field is charge. When there is electric field flowing radially, there is a source inside. Electric flux is defined as the effect of electric field over the area of the surface projected in a plane perpendicular to the field, that is (𝐸⋅
𝑛)𝑑𝐴. In order words, the electric flux of a surface which is parallel to the electric field, is equal to zero.
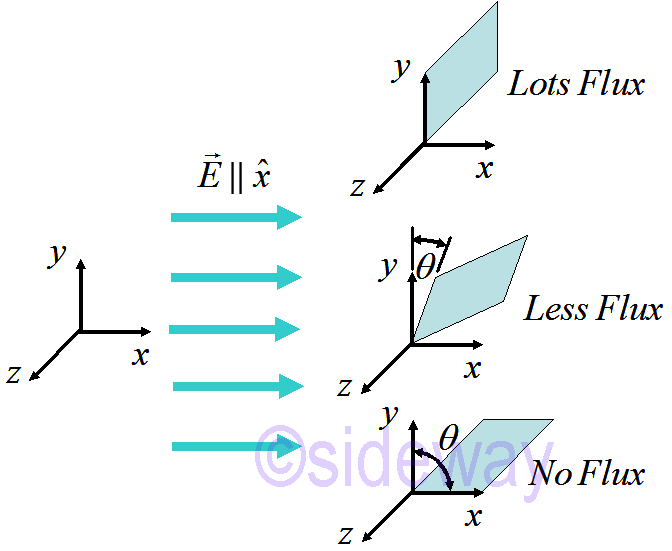 The electric flux over a surface is
The electric flux over a surface is ∑(
𝐸⋅
𝑛)𝑑𝐴.
Gauss's Law
The total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity.∮
𝐸⋅
𝑛𝑑𝐴=
1𝜀0
∑𝑞inside
Gauss's Law for Point Charge
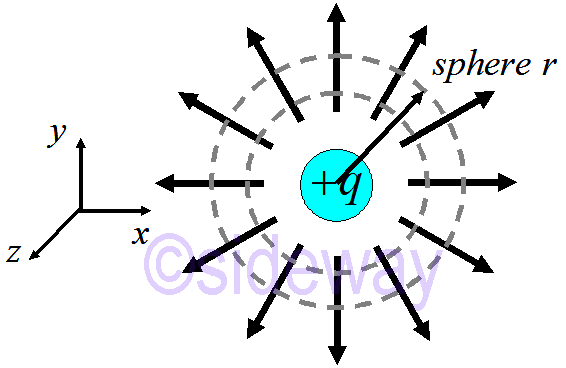 For a point charge, the electric flus of concentric spherical surface shell of radius 𝑟 is
For a point charge, the electric flus of concentric spherical surface shell of radius 𝑟 is
∮
𝐸⋅
𝑛𝑑𝐴=
14𝜋𝜀0
𝑞𝑟2(4𝜋𝑟2)=
𝑞𝜀0. The electric flux does not depend on the radius of the concentric spherical surface shell because field 𝐸∝
1𝑟2and surface area 𝐴∝𝑟2.
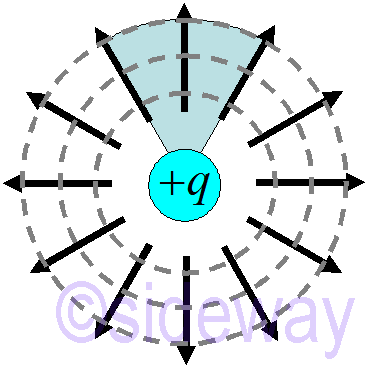 In any segment, the contribution from any shell is the same.
In any segment, the contribution from any shell is the same.
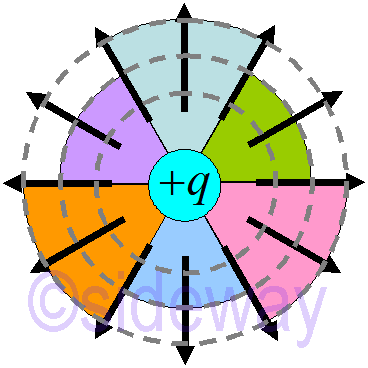 Since electric flux through any outer shell surface is always the same. The electric flux of any closed surface formed by any outer shell surfaces is always the same.
Since electric flux through any outer shell surface is always the same. The electric flux of any closed surface formed by any outer shell surfaces is always the same.
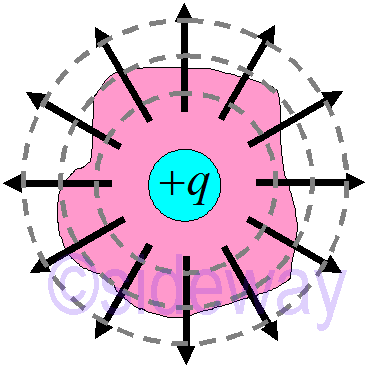 Similarly, by limit the segment to infinite small segment, the enclosed surface can be refined to surround the charge with any smooth shape by following different shperes in different places with the same electric flux.
Similarly, by limit the segment to infinite small segment, the enclosed surface can be refined to surround the charge with any smooth shape by following different shperes in different places with the same electric flux.
Gauss's Law for Plane
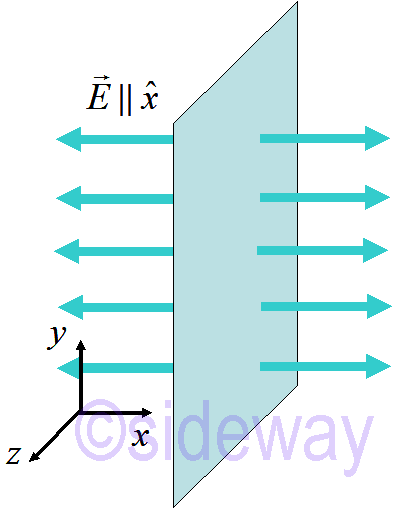 For an infinite plane with surface charge density, 𝜎=[𝑄/𝐴]. Due to geometry of plane, the electric filed is perpendicular to plane and has same magnitude everywhere.
For an infinite plane with surface charge density, 𝜎=[𝑄/𝐴]. Due to geometry of plane, the electric filed is perpendicular to plane and has same magnitude everywhere.
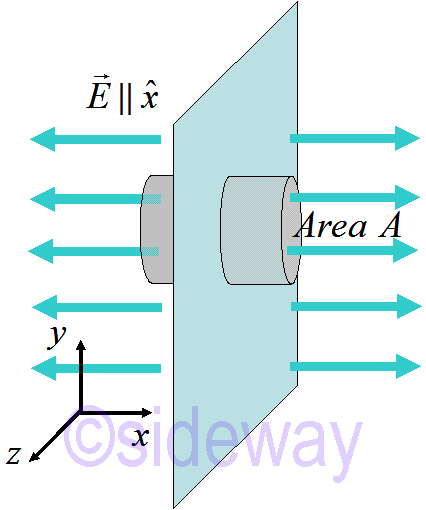 Define a Gaussian box, 𝐸 is constant and perpendicular to the two plane surfaces of the Gaussian box.
Define a Gaussian box, 𝐸 is constant and perpendicular to the two plane surfaces of the Gaussian box.
∮
𝐸
⋅𝑛
𝑑𝐴=1𝜀0
𝑞inside=[𝑄/𝐴]𝐴
𝐸(2𝐴)=1𝜀0
𝜎𝐴
𝐸=𝜎𝐴2𝜀0
Gauss's Law for Magnetism
So far, no experiment has found a magnetic charge, i.e. a magnetic monopole. Therefore 𝑞magnet=0 and Gauss's law for magnetism is∮
𝐵⋅
𝑛𝑑𝐴=0
Source and Reference
https://www.youtube.com/watch?v=ULWIQvF-muo&list=PLZ6kagz8q0bvxaUKCe2RRvU_h7wtNNxxi&index=22©sideway
ID: 200102202 Last Updated: 1/22/2020 Revision: 0
Latest Updated Links
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 37
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
