Content
Electric Field of a Ring
Electric Field along axis of a Ring
Electric Field along Axis of a disk
Infinity Charged Plane
Source and Reference
Electric Field of a Ring
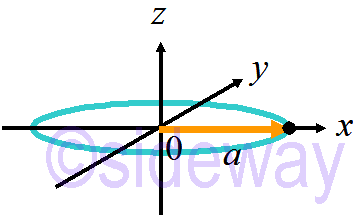
Electric Field along axis of a Ring
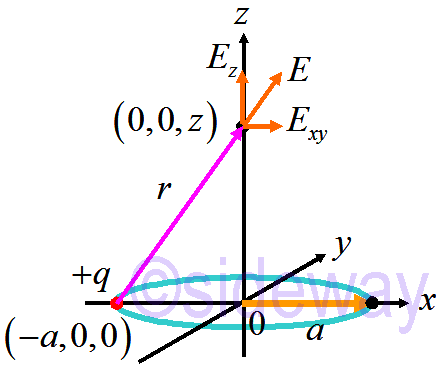 The electric field 𝐸 at ⟨0,0,𝑧⟩ with radius 𝑟 due to charged particle at ⟨-𝑎,0,0⟩ is
The electric field 𝐸 at ⟨0,0,𝑧⟩ with radius 𝑟 due to charged particle at ⟨-𝑎,0,0⟩ is
𝑟
=⟨𝑎,0,𝑧⟩⇒|𝑟|=(𝑎2+𝑧2)1/2⇒𝑟
=𝑟|𝑟|
=⟨𝑎,0,𝑧⟩(𝑎2+𝑧2)1/2
𝐸 at ⟨0,0,𝑧⟩: 𝐸
=14𝜋𝜀0
𝑞|𝑟|2
𝑟
=14𝜋𝜀0
𝑞(𝑎2+𝑧2)
⟨𝑎,0,𝑧⟩(𝑎2+𝑧2)1/2
=14𝜋𝜀0
𝑞(𝑎2+𝑧2)3/2
⟨𝑎,0,𝑧⟩
𝐸
𝑡𝑜𝑡= ∑aroundthe ring
∆𝐸𝑧𝑧
∆𝐸𝑧=14𝜋𝜀0
𝑧∆𝑞(𝑎2+𝑧2)3/2
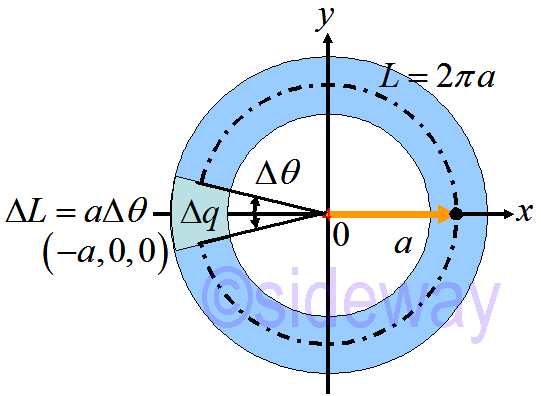 The total electric field 𝐸𝑡𝑜𝑡 at ⟨0,0,𝑧⟩ is
The total electric field 𝐸𝑡𝑜𝑡 at ⟨0,0,𝑧⟩ is
𝐿=2𝜋𝑎; ∆𝑞=𝑄2𝜋𝑎
∆𝐿=𝑄𝐿
∆𝐿
∆𝐿=𝑎∆𝜃⇒∑
∆𝐿→𝑎2𝜋∫0
𝑑𝜃=2𝜋𝑎=𝐿
⇒∆𝑞=𝑄2𝜋𝑎
𝑎∆𝜃=𝑄2𝜋
∆𝜃
⇒∑
∆𝑞→𝑄2𝜋
2𝜋∫0
𝑑𝜃
⇒𝐸𝑡𝑜𝑡 𝑧=14𝜋𝜀0
∑
𝑧∆𝑞(𝑎2+𝑧2)3/2
→14𝜋𝜀0
𝑄2𝜋
2𝜋∫0
𝑧𝑑𝜃(𝑎2+𝑧2)3/2
=14𝜋𝜀0
𝑄2𝜋
𝑧(𝑎2+𝑧2)3/2
2𝜋∫0
𝑑𝜃
=14𝜋𝜀0
𝑄𝑧(𝑎2+𝑧2)3/2
Electric Field along Axis of a disk
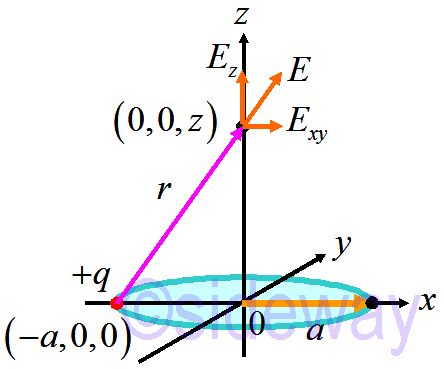 The electric field 𝐸 at ⟨0,0,𝑧⟩ with radius 𝑟 due to charged particle ∆𝑞 of ∆A=∆𝑎∆𝐿 at ⟨-𝑎,0,0⟩ is similar to that of a ring.
The electric field 𝐸 at ⟨0,0,𝑧⟩ with radius 𝑟 due to charged particle ∆𝑞 of ∆A=∆𝑎∆𝐿 at ⟨-𝑎,0,0⟩ is similar to that of a ring.
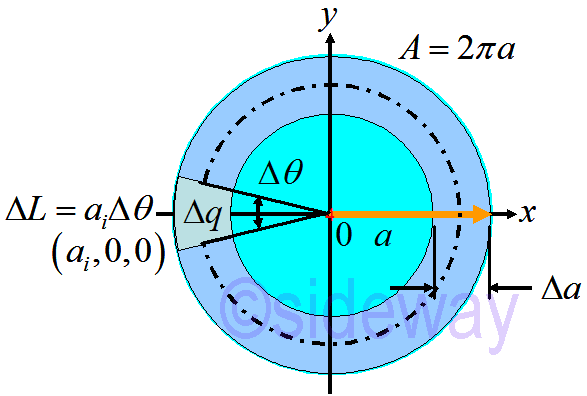 Let total net charge 𝑄 is uniformly distributed on the disk with total area 𝐴 of radius 𝑎.
Let total net charge 𝑄 is uniformly distributed on the disk with total area 𝐴 of radius 𝑎.
Total 𝑄 in area A=𝜋𝑎2
Elemental ∆𝑞𝑖 in area element ∆A𝑖=(𝑎𝑖∆𝜃)(∆𝑎)
⇒∆𝑞𝑖=𝑄𝜋𝑎2
∆A𝑖=𝑄𝜋𝑎2
(𝑎𝑖∆𝜃)(∆𝑎)
⇒ ∑𝑖
∆𝑞𝑖= ∑𝑖
𝑄𝜋𝑎2
∆A𝑖=𝑄𝜋𝑎2
∑𝑖
(𝑎𝑖∆𝜃∆𝑎)
=𝑄𝜋𝑎2
∬
(𝑎𝑖𝑑𝜃𝑑𝑎)=𝑄𝜋𝑎2
𝑎∫0
𝑎𝑑𝑎2𝜋∫0
𝑑𝜃=𝑄𝜋𝑎2
12
𝑎22𝜋=𝑄
⇒𝐸𝑡𝑜𝑡 𝑧=14𝜋𝜀0
∑
𝑧∆𝑞(𝑎2+𝑧2)3/2
→14𝜋𝜀0
𝑄𝜋𝑎2
∬
(𝑎𝑖𝑑𝜃𝑑𝑎)𝑧(𝑎2+𝑧2)3/2
=14𝜋𝜀0
𝑄𝜋𝑎2
𝑎∫0
𝑎𝑧(𝑎2+𝑧2)3/2
𝑑𝑎2𝜋∫0
𝑑𝜃=14𝜋𝜀0
𝑄𝜋𝑎2
1−𝑧𝑎2+𝑧2
2𝜋
=12𝜀0
𝑄𝜋𝑎2
1−𝑧𝑎2+𝑧2
∴𝐸
𝑡𝑜𝑡 𝑧=12𝜀0
𝑄𝜋𝑎2
1−𝑧𝑎2+𝑧2
𝑧
Infinity Charged Plane
Assume 𝑎 go to infinity, e.g. 𝑎≫𝑧𝑎→∞; 𝑄→∞ ⇒𝑄𝜋𝑎2
=𝜎 charge per unit area
𝐸
𝑡𝑜𝑡 𝑧=12𝜀0
𝑄𝜋𝑎2
1−𝑧𝑎2+𝑧2
𝑧
=12𝜀0
𝜎1−0
𝑧
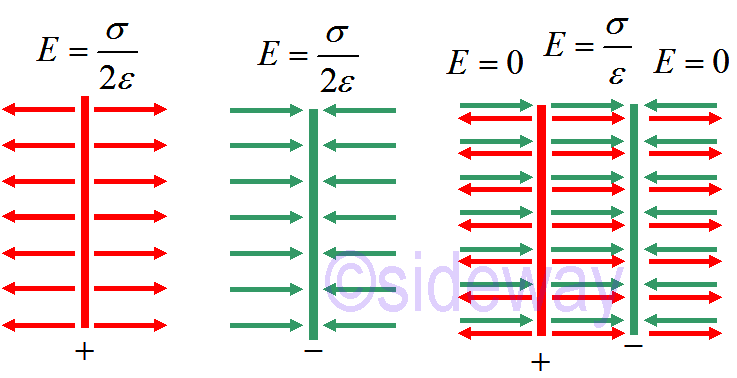
=𝜎2𝜀0
𝑧
For two parallel opposite charged infinite plane
Source and Reference
https://www.youtube.com/watch?v=WqSa620ln9M&list=PLZ6kagz8q0bvxaUKCe2RRvU_h7wtNNxxi&index=6
©sideway
ID: 191102202 Last Updated: 11/22/2019 Revision: 0
Latest Updated Links
- Travel Singapore Sight Central(last updated On 1/8/2026)
- Panasonic HHGTQ1001B13 LED Floor Light(last updated On 1/7/2026)
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 38
Reference 79
Hardware 55
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
