ElectricElectric ForcePolarizationInsulatorElectric Field of Charged RodElectric Field of Charged Ring, Disk, and PlaneElectric Field of Charged Spherical ShellPotential EnergyPotential DifferenceElectric PotentialElectric EnergyElectric CurrentMagnetic FieldKirchhoff's Current LawSteady StateCapacitor Charge and DischargeRC Circuit Time ConstantCurrent Density, ConductivityMagnetic ForceElectricity, MagnetismMotor, GeneratorGauss's LawAmpere's LawFaraday's Law, Lenz's LawSuperconductor, InductorMaxwell's EquationsWave Equation
Draft for Information Only
Content
Ampere-Maxwell Law
Maxwell's Equations
Differential Form of Gauss's Law
Differential Form of Ampere's Law
Differential Form of Maxwell's Equations
Source and Reference
Ampere-Maxwell Law
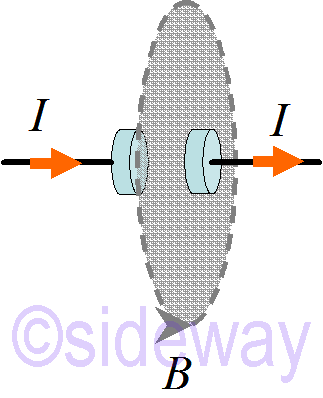 When the circuit with a capacitor is in steady state, 𝐼=0, Therefore 𝜇0
When the circuit with a capacitor is in steady state, 𝐼=0, Therefore 𝜇0∮
𝐵⋅𝑑
𝑙=0
But when the 𝐵-field is moving, 𝜇0
∮
𝐵⋅𝑑
𝑙≠0
Electric flux through this surface:
1𝜀0
𝑄𝐴𝐴=
𝑄𝜀0
The time derivative of electric flux is:
𝑑𝑑𝑡
𝑑𝑑𝑡
𝑄𝜀0≡
1𝜀0𝐼
So the changing flux acts like a current inside the capacitor. And therefore the line integral of magnetic field is.
∮
𝐵⋅𝑑
𝑙=𝜇0
∑𝐼enclosed+𝜀0
𝑑𝑑𝑡
where the first right term contributes outside the capacitor and the second right term contributes inside the capacitor.
Maxwell's Equations
∮
𝐸
⋅𝑛
𝑑𝐴=1𝜀0
∑
𝑄enclosed; Gauss's Law
∮
𝐵
⋅𝑛
𝑑𝐴=0; Gauss's Law (Magnetism)
∮
𝐸
⋅𝑑𝑙
=−𝑑𝑑𝑡
∫
𝐵
⋅𝑛
𝑑𝐴; Faraday's Law
∮
𝐵
⋅𝑑𝑙
=𝜇0∑
𝐼enclosed+𝜀0𝑑𝑑𝑡
∫ 𝐸⋅𝑛𝑑𝐴𝐹=𝑞
𝐸+𝑞
𝑣×
𝐵
Differential Form of Gauss's Law
Gauss's Law:∮
𝐸⋅
𝑛𝑑𝐴=
1𝜀0
∑𝑄enclosed
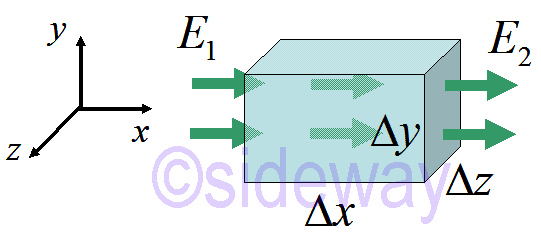 Consider a region of space, enclosed by a box ∆𝑉.
Consider a region of space, enclosed by a box ∆𝑉.Lim∆𝑉→0
𝐸⋅
𝑛𝑑𝐴∆𝑉
Lim∆𝑉→0
1𝜀0
∑𝑄enclosed∆𝑉≡
1𝜀0𝜌
⇒
Lim∆𝑉→0
𝐸⋅
𝑛𝑑𝐴∆𝑉
Lim∆𝑉→0
(𝐸2−𝐸1)∆𝑦∆𝑧∆𝑥∆𝑦∆𝑧=
Lim∆𝑥→0
(𝐸2−𝐸1)∆𝑥≡
∂𝐸𝑥∂𝑥=
1𝜀0𝜌
for a general case where 𝐸 can point in any direction:
∂𝐸𝑥∂𝑥+
∂𝐸𝑦∂𝑦+
∂𝐸𝑧∂𝑧≡
∇⋅
𝐸=
1𝜀0𝜌 The parallel derivative of Gauss's Law differential form where
∇≡
∂∂𝑥,
∂∂𝑦,
∂∂𝑧
Differential Form of Ampere's Law
Ampere-Maxwell Law:∮
𝐵⋅𝑑
𝑙=𝜇0
∑𝐼enclosed+𝜀0
𝑑𝑑𝑡
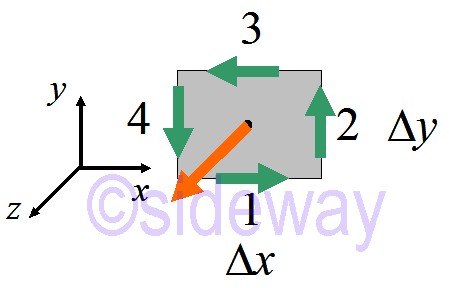 Consider a region of area, enclosed by a box ∆𝐴 and express 𝐼 in term of
Consider a region of area, enclosed by a box ∆𝐴 and express 𝐼 in term of 𝐽⋅
𝑛∆𝐴.
Lim∆𝐴→0
𝐵⋅𝑑
𝑙∆𝐴
Lim∆𝐴→0
𝐽⋅
𝑛∆𝐴∆𝐴
Lim∆𝐴→0
𝑑𝑑𝑡
∫𝜇0𝜀0=𝐸⋅𝑛𝑑𝐴∆𝐴
Lim∆𝐴→0
𝜇0𝐽𝑧∆𝐴∆𝐴+
Lim∆𝐴→0
𝑑𝑑𝑡
𝐸𝑧∆𝐴∆𝐴𝜇0𝜀0
⇒
Lim∆𝐴→0
𝐵⋅𝑑
𝑙∆𝐴
𝐽𝑧+
𝑑𝐸𝑧𝑑𝑡𝜇0𝜀0
⇒
Lim∆𝐴→0
𝐵⋅𝑑
𝑙∆𝐴
Lim∆𝐴→0
(𝐵1,𝑥−𝐵3,𝑥)∆𝑥+(𝐵2,𝑦−𝐵4,𝑦)∆𝑦∆𝑥∆𝑦=𝜇0
𝐽𝑧+
𝑑𝐸𝑧𝑑𝑡𝜇0𝜀0
⇒
Lim∆𝐴→0
𝐵⋅𝑑
𝑙∆𝐴
Lim∆𝑦→0
(𝐵1,𝑥−𝐵3,𝑥)∆𝑦
Lim∆𝑥→0
(𝐵2,𝑦−𝐵4,𝑦)∆𝑥=−
∂𝐵𝑥∂𝑦+
∂𝐵𝑦∂𝑥=𝜇0
𝐽𝑧+
𝑑𝐸𝑧𝑑𝑡𝜇0𝜀0
crossed derivatives: −
∂𝐵𝑥∂𝑦+
∂𝐵𝑦∂𝑥
For a loop in any direction, this can be re-expressed as:
∂𝐵𝑧∂𝑦−
∂𝐵𝑦∂𝑧
∂𝐵𝑥∂𝑧−
∂𝐵𝑧∂𝑥
∂𝐵𝑦∂𝑥−
∂𝐵𝑥∂𝑦
∇×
𝐵=𝜇0
𝐽+𝜀0
∂𝐸∂𝑡
Differential Form of Maxwell's Equations
Divergence for enclosed flux:
∇
⋅𝐸
=1𝜀0
𝜌 for ∮
𝐸
⋅𝑛
𝑑𝐴=1𝜀0
∑
𝑄enclosed; Gauss's Law
∇
⋅𝐵
=0 for ∮
𝐵
⋅𝑛
𝑑𝐴=0; Gauss's Law (Magnetism)
Curl for Circulation:
∇
×𝐸
=−∂𝐵∂𝑡
for ∮
𝐸
⋅𝑑𝑙
=−𝑑𝑑𝑡
∫
𝐵
⋅𝑛
𝑑𝐴; Faraday's Law
∇
×𝐵
=𝜇0𝐽
+𝜀0∂𝐸∂𝑡
∮
𝐵
⋅𝑑𝑙
=𝜇0∑𝐼enclosed+𝜀0𝑑𝑑𝑡∫ 𝐸⋅𝑛𝑑𝐴
; Ampere-Maxwell Law
Source and Reference
https://www.youtube.com/watch?v=fkfnDopQBYQ&list=PLZ6kagz8q0bvxaUKCe2RRvU_h7wtNNxxi&index=26©sideway
ID: 200200502 Last Updated: 2/5/2020 Revision: 0
Latest Updated Links
- Travel Singapore Sight Mandai(last updated On 12/8/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/7/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 24
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
